Written by Cremieux Recueil.
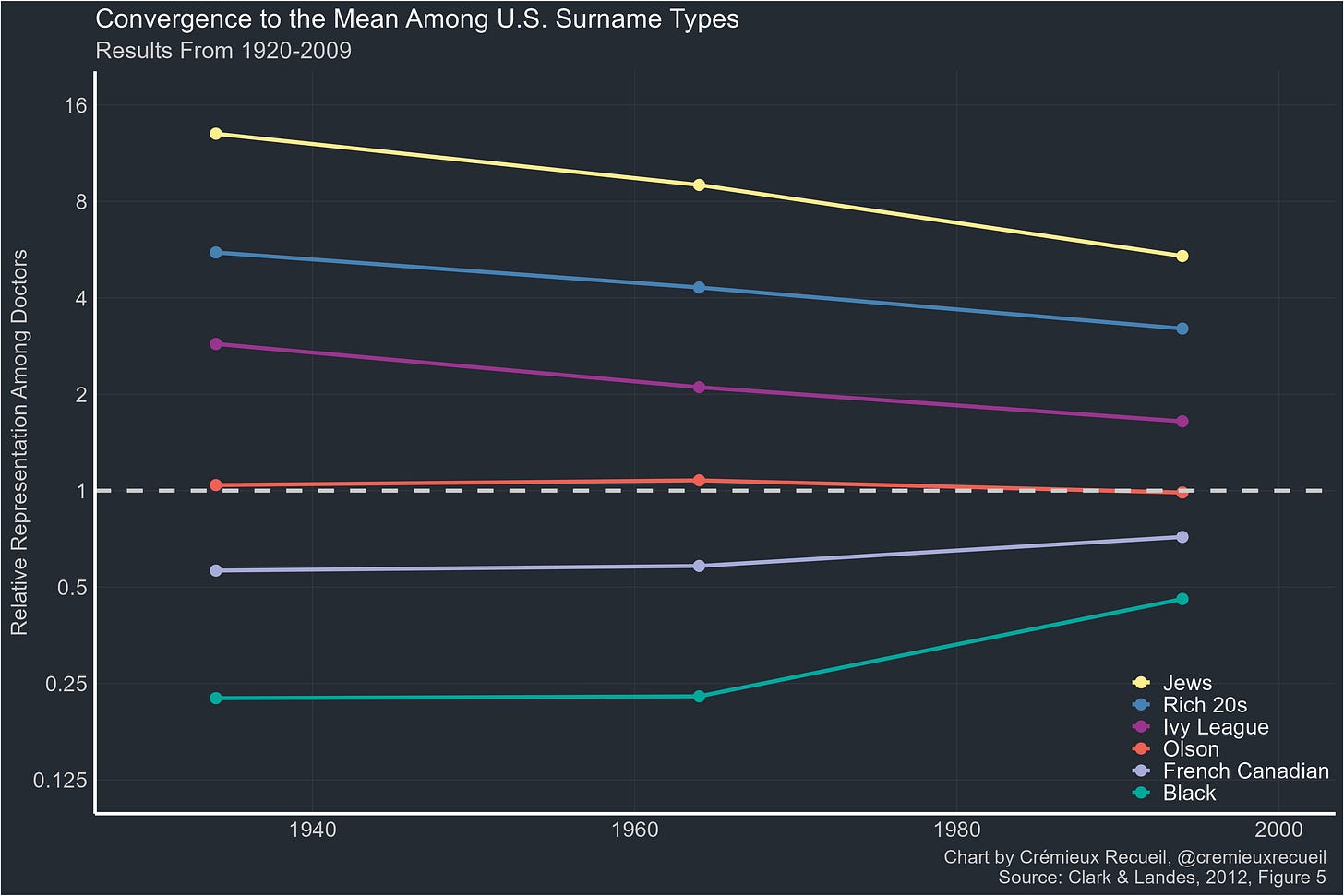
Most men don’t pick their surnames. Because of this fact, surnames carry a lot of information. They can be used to predict social status and to track it across generations. For example, the relative representation of doctors within a lineage can give an approximate indication of that lineage’s social status. Here’s how that quantity looks in six U.S. groups:
Notice anything? First, it’s clear that Blacks caught up after the 1960s. Second, some lineages have been close to average for almost a century now. Third, there are a lot of Jewish doctors. Or at least there were a lot of Jewish doctors. That change over time becomes a little clearer when the y-axis is no longer logged:
This is a stunning decline, but it’s not without precedent. As Tablet Mag tells us, Jews are vanishing from American life (though the cases discussed in their article were probably too rapid to have been due to the processes underlying the change in the chart above). Despite this reality, Jews are still high-achieving. Their high achievement has always struck observers as something of a puzzle. After all, who has suffered more persecution in history than Jews?
Today, Jewish population shares are an ‘index of opportunity’ – the more Jews in an area, the more prosperous it seems to be. We can’t be sure this relationship is causal, but why shouldn't it be, at least partially? After all, Jews are overrepresented among geniuses, innovators, and other significant figures.
To witness such overrepresentation, you only need to look at chess champions, bridge players, Nobel and Wolf prize winners, Fields medalists, and the winners of basically any prize for objectively-important work.1 One interesting way to measure this is bibliometrically. In his book Human Accomplishment, Charles Murray looked at different encyclopedias and counted significant figures in them, allowing him to quantify the contributions of different ethnicities, nationalities, etc. to human achievement in different areas. This approach does have limitations, but it also has obvious upsides: there aren’t going to be many people whose inventions and contributions are misattributed, and if someone came up with an innovation recently, they’re unlikely to go unacknowledged. Moreover, the results of Human Accomplishment have been confirmed by other sources, which yield plots like this one from de Courson, Thouzeau & Baumard (2023):
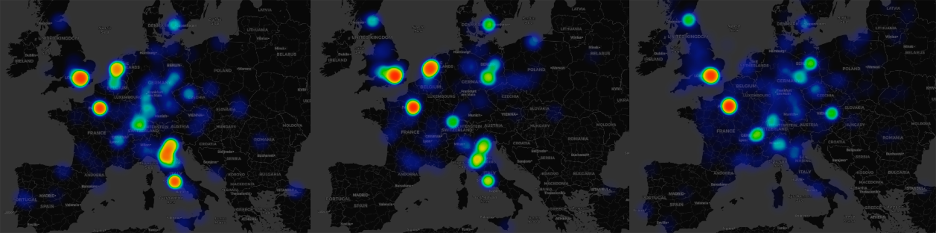
What do these sources say about Jews? Simply that, despite being a small percentage of the population, their emancipation in the 19th century—when they stopped being religiously isolated and joined the wider European society—was associated with a rapid increase in their representation among significant figures. Consider this chart taken from Human Accomplishment:
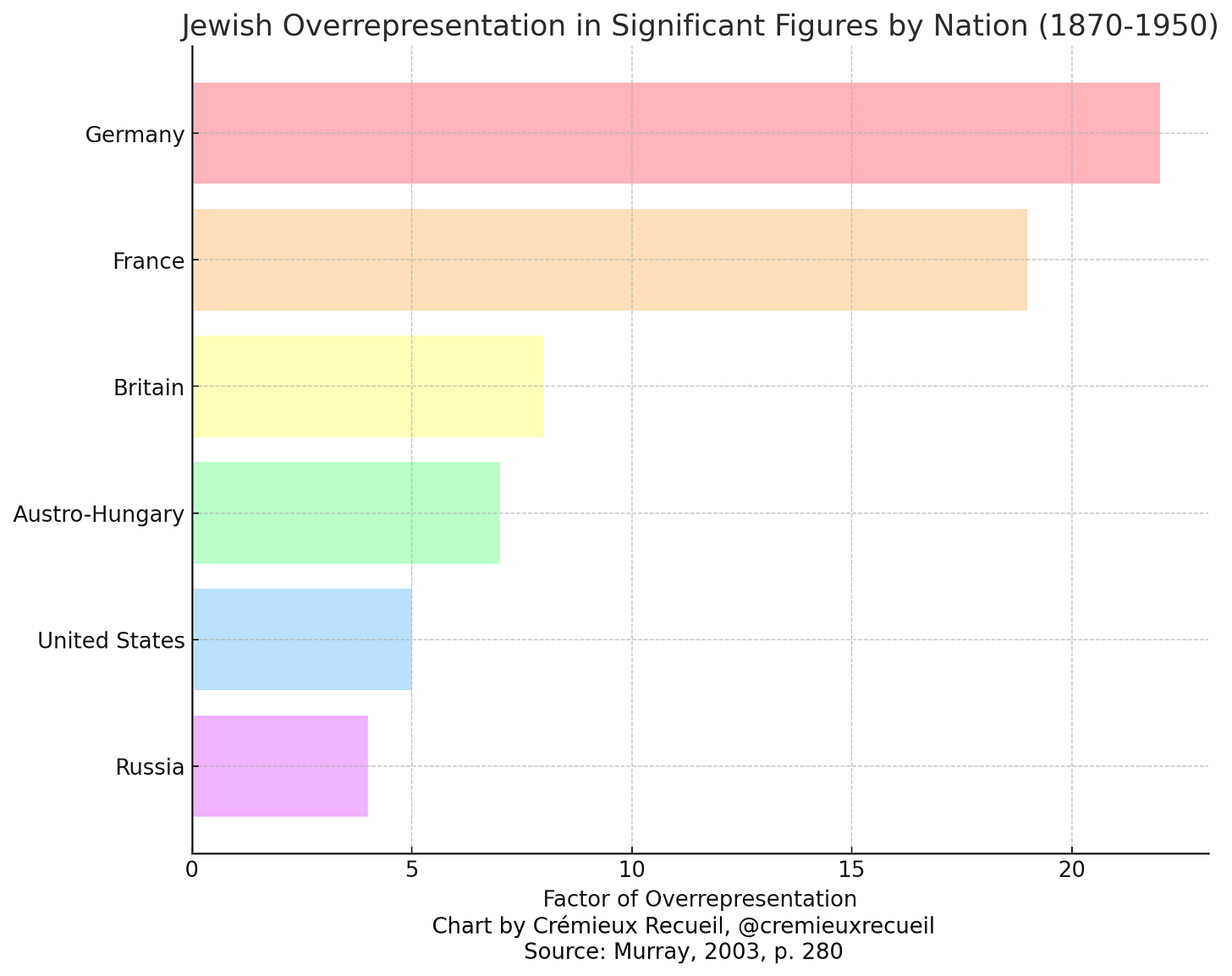
In the period between 1870 and 1950, the level of Jewish overrepresentation is simply remarkable. Across a variety of fields of achievement, Jews came to be vastly overrepresented among significant figures:
Plotting these data not by field but by nation makes for another interesting result:
Exceptional Jewish achievement wasn’t confined to the period immediately after Jews were emancipated. In several fields, it actually increased in the latter half of the 20th century.
These kinds of figures demand an explanation, and an eminently plausible one is that Jews are very smart.
How Smart Are Jews?
When people talk about Jewish smarts, they’re generally not talking about all the nearly fifteen million of the world’s Jews; they’re talking about the Ashkenazi (Central/Eastern European) Jewish population, which makes up the overwhelming majority of the Jews living in the United States and a substantial minority of those living in Israel. How overwhelming the American majority is depends on who, when, and how you ask.
The standard figure is that Ashkenazim make up 90-95% of the U.S. Jewish population. Mizrahim (Arab Jews), Sephardim (Southern European Jews) and other Jewish groups have had a historically limited presence in the U.S. thanks to America’s immigration laws. Conversions are also rare – though the relevant statistics can be misleading.
Simply asking Jews if they’re Ashkenazi might give us a decent estimate of the percentage of American Jews who belongs to that particular group. However, that question often conflates ethnicity and tradition, which matters because a large proportion of Jews aren’t really religious. So when just 66% of American Jews identify as Ashkenazi, that’s likely a lower-bound. The same survey allows us to set an upper-bound on America’s Ashkenazi Jewish share based on racial self-identification. 92% of Jews identify as White, 1% as Black, 4% as Hispanic, and the remainder as Asian, Amerindian/Alaska Native, Hawaiian/Pacific Islander, another race, or multiracial. And if they’re not White (or perhaps Hispanic), they’re obviously not Ashkenazi. Note that self-identified race varies by age among Jews. Among Jews aged 65+, 97% identify as White, followed by 96% of Jews aged 50-64, 88% of Jews aged 30-49, and 85% of Jews aged 18-29. The main reason the younger groups identify as less White is that they identify as Hispanic and multiracial, due to outbreeding and, perhaps, non-White Jewish immigration.
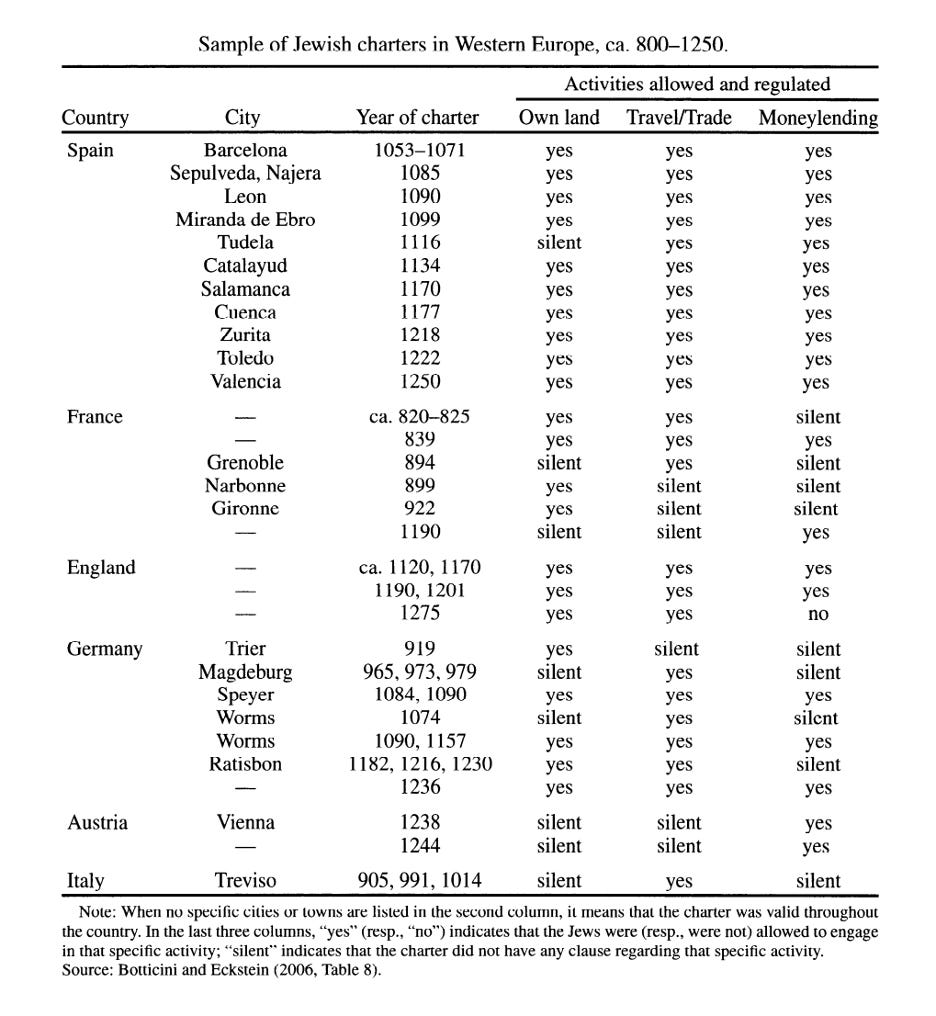
Since Ashkenazi Jews are the group for which we have the most evidence of high intelligence, they will be the focus of this section. Before getting to the psychometric results, it’s worth noting that the story of Jewish success predates modernity by more than a thousand years – as I noted in a previous article. One of the telltale signs that Jewish success isn’t new is that medieval European Jewish charters had provisions specifically regulating Jewish operation and entry into high-IQ professions like trading and moneylending.
During the Spanish Inquisition, Jews were less likely to engage in the practice of age heaping when reporting their birthdays – a rough marker of numeracy – and they were more literate too. Jews also made fewer errors when they were being interrogated by members of the Inquisition. The way this worked is that inquisitors would ask people for their ages and then to provide detailed reconstructions of their life narratives up to that point. If a person made a mistake in telling their story, the inquisitor conducting the interview would notice and accuse the interviewee of lying. For example, imagine you’re a man who claims to be thirty years old. If your story is that you married at age twenty and worked for fifteen years on a farm after that, the inquisitor would have no problem identifying that your story is inconsistent.
Ashkenazi achievement was first recognized in a major way after Jewish emancipation. Consider what Lord Ashley stated in his 1847 address to the British House of Commons:
The Jews are a people of very powerful intellect… [They have] presented… in proportion to their numbers, a far larger list of men of genius and learning than could be exhibited by any Gentile country. Music, poetry, medicine, astronomy, occupied their attention, and in every field, they were more than a match for their competitors.
The controversial anthropologist Joseph-Arthur Comte de Gobineau ranked Jews alongside “Aryans” for their achievements. Francis Galton noted that they were “rich in families of high intellectual breeds”. Madison Marsh praised their “high average intelligence”. Mark Twain famously commended Jews for surviving a history filled with hatred, while also claiming they were underrepresented among American soldiers. He was later shown that Jews were in fact overrepresented in the U.S. military, leading him to retract his statement from Concerning the Jews, and to release a postscript: The Jew as Soldier.
Close observers throughout the ages have been aware of exceptional Jewish achievement. And after emancipation – when it became possible for Jews to succeed in various new domains – such awareness became widespread. But has anyone attempted to quantify Jewish intelligence? The answer is yes, and in many different ways. Let’s begin with the always-insightful pseudonymous commentator, La Griffe du Lion.
La Griffe’s Proxy Estimations of Jewish Ability
La Griffe wrote three articles dealing with Jewish intelligence between February 2000 and September 2003. The first post began with some curious data. Take a look:
Although Jews made up just 2% of the U.S. population at the time, almost every other category was far more Jewish. For La Griffe, the obvious reason for this overrepresentation in these areas of achievement and distinction was high Jewish intelligence. There are six categories where La Griffe argued intelligence is most relevant: Westinghouse Science Prize winners, faculty at elite colleges, Supreme Court law clerks, Ivy Leaguers, ACM Turing Award winners, and Nobel Prize-winning Americans. And across these six, the average proportion of Jews was 27%, with little variation. La Griffe showed that knowing only the proportion of Jews in these areas of high achievement, in the population, and armed with an IQ estimate and the assumption that Nobel Prizes are awarded in line with intelligence, one could produce a plausible estimate of the IQs of Jewish and non-Jewish Nobel laureates without needing to test anyone. This rounded out to about 145 assuming a mean Jewish IQ of 115; with a mean Jewish IQ of 112, it would be 136, and with a mean Jewish IQ of 108, it would be 124.
The second post sought to derive an actual estimate of Jewish IQ, rather than assuming what it was to estimate another quantity. It began with an observation: City College of New York is generally unremarkable, except for its eight Nobel Prize-winning alumni. Strikingly, these seven scientists and one economist all graduated between 1933 and 1954, despite minimal entry requirements. At the time, the school didn’t even have any notable faculty members, it didn’t charge tuition, and it was just a subway ride away for most New Yorkers. What made CCNY so exceptional is what makes elite institutions successful in general: the quality of their people.
By 1910, New York had become 25% Jewish. And by the early 1930s, CCNY had become 80% Jewish. Counting the laureates, every single one was Jewish. In the period just before this, circa 1912-33, Americans earned 93 serious Nobels (i.e., not Peace or Literature), and 25 of the receiving laureates were Jewish. Since about half of all American Jews at the time lived in New York City, it’s reasonable to expect half the laureates to be New Yorkers. If half of the best Jewish students in New York City went to CCNY, then we might expect six Jewish laureates between 1933 and 1954; eight therefore no longer seems that astounding. The assumption that so many exceptional Jews went to CCNY is, of course, very reasonable: many Jews were the children of poor immigrants, so free tuition made university attendance possible; and Jews were the targets of discriminatory quotas at other universities. As that era’s discrimination faded and admission standard’s fell, CCNY’s prominence also declined as other universities snagged the brightest Jews.
We can estimate the IQs of CCNY’s Jewish and non-Jewish students, and the general population of Jews. All we need to know are a few numbers about the size of the student body and the demographics of New York City. We also need to make two assumptions: out-of-towners aren’t relevant for the admissions pool, and admissions were about equally meritocratic for all groups. These assumptions seem reasonable.
80% of CCNY’s 1930 student cohort were Jews, so the non-Jewish fraction was 20%. To estimate the number of slots, we can use the number matriculating to degrees as a lower-bound and 1,000 as an upper-bound. With normality and equal variances, Jewish students would have had an IQ of between 139 and 142, given a non-Jewish general population mean of 100 with a standard deviation of 15. Such a high class mean wasn’t actually so unusual in the past.
What’s more, we can obtain another set of bounds that places the Jewish general population IQ at an IQ of 114 to 115. The graduates of the university would have had a mean of 144 to 147 for Jews and 145 to 148 for non-Jews, meaning that they were a minimum of 2.7 standard deviations above the non-Jewish mean and 1.7 standard deviations above the Jewish mean. CCNY’s Jewish graduates were emblematic of the top 4-5% of the Jewish population at the time: “You don’t get eight Nobel Prize winners from nothing!”
In a third article, La Griffe responded directly to Kevin MacDonald. He laid out what would be required to estimate the intelligence of Ashkenazi Jews using real-life performance. Specifically:
A group must be found whose membership depends purely on cognitive ability.
The group must be unequivocally defined.
The percentage of group members comprising Ashkenazim and non-Jewish Whites must be established.
Both Jews and non-Jews must have the opportunity to become group members (if Jews are forbidden, estimation will be biased).
Both Jews and non-Jews must be motivated to become group members.
La Griffe identified such a group: Participants in the USSR Chess Championships. There were data for 1947-49 and 1970-76. At this time, Jewish participants were mentioned 83 times and non-Jewish participants were mentioned 110 times. Given the Jewish population of roughly two million out of the Soviet Union’s 230 million total, Jews would have been 88 times more likely than non-Jews to participate, giving us an estimated Jewish mean 1.06 standard deviations above the non-Jewish mean. And if non-Jewish Russians have an IQ of 96, that means Ashkenazi Jews have a mean of 112.
La Griffe used Fields Medalists to perform a similar calculation. 38 winners at the time of his article were non-Jewish Whites and 13 were Ashkenazi Jews. Assuming populations of 13 million for Ashkenazim and 1 billion for non-Jewish Whites, the Ashkenazi mathematical IQ came out to 111. And using the results of the William Lowell Putnam Competition, he came up with an estimate of 110 for their overall IQ.
Of course, there’s always the chance that proxies like those discussed above overstate or understate Jewish achievement. And they’re not actually needed for the simple reason that Jews have been given psychometric tests. We do know how smart Ashkenazi Jews are, and we probably know how smart other Jewish groups are too.
The Psychometric Measurement of Jewish Ability
In 2011, Richard Lynn published The Chosen People, a compendium of statistics on Jewish achievement the world over. His book is a good starting point for gathering Jewish IQ test results since it lists most of them.
The Chosen People lists ten different Jewish IQ estimates for Britain from: Davies & Hughes (1927; 3 results), Winch (1930), Vincent (1966), Lynn & Longley (2006; 2 results), and three DfES test results for the year 2004. Davies & Hughes’ results were three different test results with the same sample, Lynn & Longley’s were two different test results with different samples, and the DfES test results all used one sample with three different tests. Accordingly, we’ll go the simple route and take their means and then perform a psychometric meta-analysis of the resulting six datapoints. For the DfES results, it's assumed that the Jewish variance is equal to the variance for Gentiles since those scores could only be computed through comparing pass rates. The result was an estimated average IQ of 110.9 for British Jews (who are typically cited as 80-90% Ashkenazi) with a meta-analytic sample size of 3,257 Jews.2
The next country for which Lynn’s book provides IQ estimates is Canada. There were nine in total from: Wendt & Burwell (1964; 3 results), Majoribanks (1972; 5 results), and the Toronto Star (1995). Wendt & Burwell’s results were independent administrations of the WISC to different samples. Majoribanks’ analyses involved giving 100 Jews, 100 Protestant Anglos, and 100 French Canadians a series of tests, and thus these datapoints were not independent. Unfortunately, the Toronto Star did not include sample sizes, but theirs was likely the largest of the three sources. Using just Wendt & Burwell’s and Majoribanks’ results, the average IQ among Canadian Jews (who are overwhelmingly Ashkenazi) is 108.7 with a meta-analytic sample size of 206.3 The Toronto Star result was consistent with an IQ of 106.2. The simple average would thus be an IQ of 107.9.
Two other countries worth mentioning are South Africa and Serbia. Regarding the former, Lynn noted that pass rates on the university matriculation exam were consistent with Jews having a 13.4-point advantage over non-Jewish Whites. The Serbian result comes from Lynn & Čvorović (2015), who went to Serbia and gave Raven’s matrices to a sample from the country’s dwindling Jewish community. At the time of the study, there were less than 1,200 Jews left in the whole country, with prior emigration and sampling likely having been selective. The sample included 30 self-identified Sephardim, 22 Ashkenazim, and 84 people who identified as “mixed”. The Sephardim obtained a U.S.-normed score of 102.3 and the Ashkenazim scored 105.8.4
Most psychometric testing data from outside Israel comes from the U.S. Some of the earliest studies from the U.S. are now over a century old, and are almost certainly biased because they’re based on tests of immigrants who spoke English as a second language. I will therefore omit them. Consulting Lynn’s list, this eliminates studies like Murdoch (1920), Jordan (1921), Feingold (1924), and Rigg (1928).
The earliest usable result is given by Bailey (1922), followed by Terman (1924), Luckey (1925), Goodenough (1926), Cohen (1927), Garrett (1929), Maller (1933), Pintner & Artensian (1936), Held (1941), Shuey (1942), Brown (1944), Nardi (1948), Sheldon (1954), Solomon (1956), Levinson (1957; 2 results), Miner (1957), Levinson (1958), Levinson (1959; monolingual results only due to test bias among bilinguals), Levinson (1960), Project Talent, Gross (1969; 4 results), Bachman (1970), Romanoff (1976), Levinson & Block (1977), the Project Talent Aging Study, Gross (1986), Herrnstein & Murray (1994), Fejgin (1995; 2 results), College Board (2002)5, Lynn (2004), Lynn & Kanazawa (2008), Nyborg (2009), Fuerst (2013), Dunkel et al. (2015; 2 results), Fuerst (2015), Dunkel et al. (2019)6, Kirkegaard & Lasker (2020), and Fuerst, Shibaev & Kirkegaard (2023). A few of these results do not have sample sizes, and will therefore be excluded from the meta-analysis.
Meta-analysis yields an estimated American Jewish IQ of 110, based on 22,653 Jews and many more Gentiles.7 But this slightly understates the average for the simple reason that four of the studies had selected samples comprising university students. Recall from La Griffe’s CCNY example how close the estimated IQs of Jewish and Gentile CCNY students were, despite large differences between the general populations. We therefore have to exclude Cohen (1927), Garrett (1929), Held (1941), and Shuey (1942). We should also remove Lynn (2004) because its data is a subset of Lynn & Kanazawa’s (2008). Likewise, the PTAS should be removed because its data is just a subset of the original Project Talent data. These omissions reduce the sample size, but only by 1,847. And importantly, they minimally change the American Jewish IQ estimate, which becomes 110.1.
And there we have it: psychometric test results from outside of Israel indicate the average IQ among Ashkenazi Jews is substantially higher than among non-Jewish whites. Meta-analyzing all the relevant studies above yields a figure of 110.20. The simple average excluding university student comparisons is approximately the same at 110.03.
But let’s not be too hasty: a lot of these studies were small, and that can cause major issues in meta-analyses. There is no evidence of publication bias or trends over time (unweighted: -0.0146, p = 0.466; -weighted: -0.026, p = 0.100)8, but there’s still some chance that the result is over- or understating Jewish intelligence due to the inherent noisiness of small samples, and perhaps even bias in the measures or the effects of unmodeled specific abilities. However, a solution is available: Project Talent, an enormous sample of almost 5% of the high school students in the U.S. in 1960.
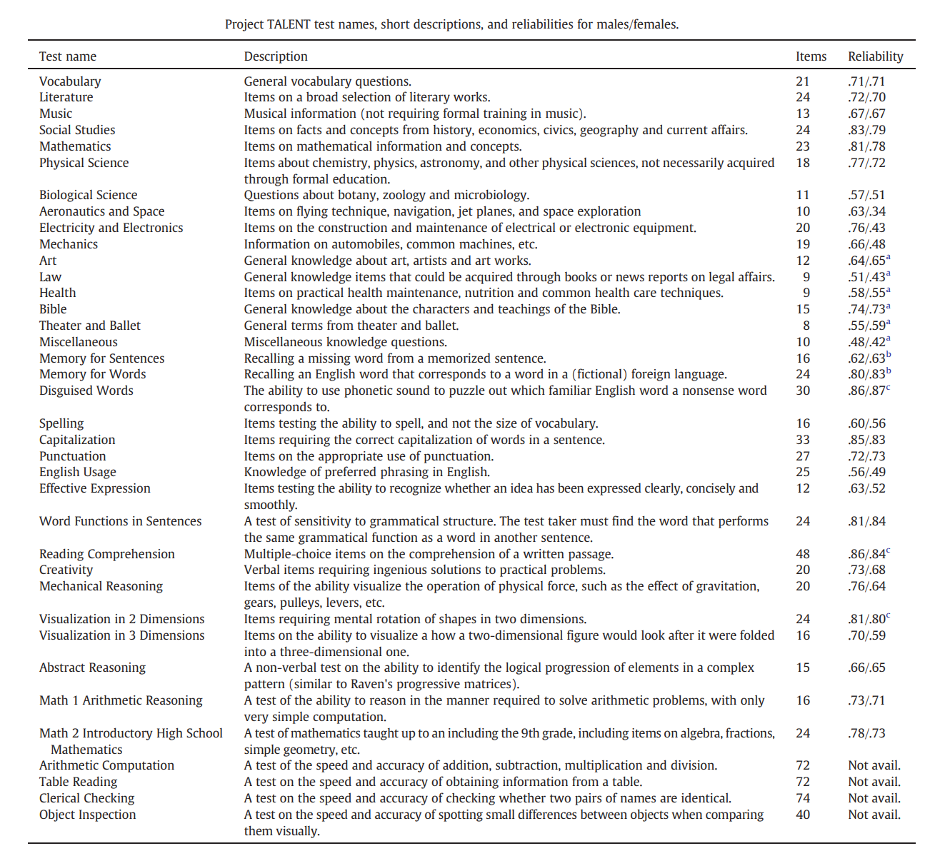
Project Talent is a population-representative sample with unusually high-quality cognitive testing. For this reason, it has been used extensively in the field of intelligence research. If you’re well-versed in the field, you will understand why by scrutinizing the table listing the tests I will be analysing:
If you’re not well-versed in the field of intelligence research, let me assure you: that’s an unusually rich battery of tests. Before getting to the analysis, it’s important to understand what this means. First, it means the same thing as any other test battery. The reason for this is that cognitive test results are universally positively correlated (‘the positive manifold’) and all cognitive tests tap general intelligence (‘the indifference of the indicator’), coupled with the fact noted by Wilks (1938) that the correlation of linear composites approaches one when the variables constituting them are positively correlated and all the weights are positive. This is why it is often appropriate to use ‘proxies’ or singular tests to measure group means: so long as the test has sufficient reliability and validity, there’s no psychometric bias, and the ability residual of g isn’t systematic with respect to group membership for some measure, we can derive high-quality measurements of g. And that’s why things like SAT scores are often great for estimating groups’ IQs. Second, it means we don’t have to focus solely on general intelligence; we can investigate whether there are differences in specific skills, like spatial and verbal ability. (Some people have argued that the Jewish IQ advantage is primarily about verbal ability.)
For the purpose of this article, I analyzed the battery of tests with the model proposed by Major, Johnson & Deary (2012), the so-called “verbal-perceptual-image rotation” model (g-VPR). And I analyzed scores across grade levels for four groups: Non-Jewish Whites (n = 118,696), Jewish Whites (8,471), Asians (947), and Blacks (5,618), without Hispanics. All subtests were controlled for participant age9 and sex prior to any estimation.10
Through multi-group confirmatory factor analysis, the modeled means for g, relative to a White score of 100, were 101.2 for Asians11, 82.0 for Blacks, and 113.0 for Jews. An obvious question to ask is how much of this is attributable to differences in socioeconomic status (SES). After all, by the time this sample was gathered, American Jews had risen out of poverty and reached high levels of socioeconomic attainment. Adjustment for SES is not straightforward, however, as it is both a cause and a consequence of IQ. Consider each group’s scores for g stratified across deciles of SES, calculated in common for the whole sample:
The Jewish advantage over non-Jewish Whites seems to be practically constant across different SES deciles, significantly increasing (interaction = 0.13995, p = 0.00524) with SES. The slope for Asians and Whites is not significantly different (0.03444, p = 0.47), but this might be due to Asians’ small sample size. The slope for Blacks, on the other hand, is shallower than for the other groups (-0.113, p = 0.015, so this is marginal). In terms of correlations, the relationship between SES and IQ is r = 0.42 for Asians and Non-Jewish Whites, 0.46 for Jews, and 0.39 for Blacks. Because differentially-functioning causes can be ruled out by measurement invariance the upper-bound effect of SES (in the absence of suppression or measurement error) is the lowest we can see, equivalent to a correlation of 0.39. But this is still quite likely to be an overestimate of the causal effect of SES, as we know from adoption, lottery, twin, and longitudinal studies.
Nevertheless, the d between Blacks and Jews for SES is 1.46 (in Black SDs, the gap is 1.4 SDs in size). So if Blacks had Jewish levels of SES, and the causal effect of the latter is equal to r = 0.39, the Black IQ would be 90.1 using the White g SD, and 90.4 using the Black/Asian SD. The Asian IQ would be 106.0 using the White SD and 106.1 using the Black/Asian SD. And the white IQ would be 103.2. As a matter of fact, Jewish and Asian cognitive advantages are not plausibly due to SES (nor are Black deficits). It is worth noting that, Asians outperformed Whites despite having 0.269 d lower SES.
It's quite clear that Jews have higher average intelligence than other groups. More importantly, the Jewish advantage is primarily an advantage in g, consistent with Spearman’s hypothesis. But other differences also exist, and they are worth discussing.
Relative to Whites, Blacks had higher mathematical (0.279 g) and mechanical/science (0.233 g) ability net of g, but as is typically observed, they had substantially lower perceptual ability – which is, roughly-speaking, a measure of spatial ability (-0.654 g). Asians too had relatively higher mathematical (0.428 g) and mechanical/science (0.137 g), and they had the same perceptual ability. Finally, Jews had relatively higher mathematical (0.245 g) and mechanical/science (0.218 g) ability, in addition to lower perceptual ability (-0.551 g).
It’s often assumed that Jews show a major discrepancy between verbal and spatial ability, scoring very high on the former and rather low on the latter. Richard Nisbett described this pattern in Intelligence and How to Get It:
It is important to note: Burg and Belmont, 1990; Ortar, 1967; Patai, 1977. Before leaving the topic of Jewish IQ, I should note that there is an anomaly concerning Jewish intelligence. The major random samples of Americans having large numbers of Jewish participants show that whereas verbal and mathematical IQ run 10 to 15 points above the non-Jewish average, scores on tests requiring spatial-relations ability (ability to mentally manipulate objects in two- and three-dimensional space) are about 10 points below the non-Jewish average (Flynn, 1991a). This is an absolutely enormous discrepancy and I know of no ethnic group that comes close to having this 20 to 25-point difference among Jews. I do not for a minute doubt that the discrepancy is real. I know half a dozen Jews who are at the top of their fields who are as likely to turn in the wrong direction as in the right direction when leaving a restaurant. The single ethnic difference that I believe is likely to have a genetic basis is the relative Jewish incapacity for spatial reasoning. I have no theory about why this should be the case, but I note that it casts an interesting light on the Jews’ wandering in the desert for forty years!
These claims are not actually well-supported. What the Jewish “verbal-spatial” discrepancy represents is, in fact, just a spatial deficit and a g advantage, where verbal tests are generally more g-loaded and spatial ability is less correlated with other subdimensions of intelligence than is verbal ability. If there appears to be a large Jewish spatial deficit, it’s likely such a deficit is due to test bias, with the true deficit being smaller than people like Nisbett have claimed.
Careful readers will have noticed that all the data discussed so far comes from samples collected outside of Israel – which is home to a large percentage of the world’s Jews. That’s because data from Israeli IQ testing is controversial. But to gain a full understanding of Jewish intelligence, we must examine it.
The Psychometric Measurement of Jewish Ability, in Israel
As mentioned in the previous section, people are primarily interested in the intelligence of Ashkenazi Jews, rather than the intelligence of Sephardim, Mizrahim, Falasha (Ethiopians), or other smaller Jewish groups. Israel has more Jews than any other country, but many of them aren’t Ashkenazi. This fact becomes evident when a few facts are considered. First, here’s the population of Israel and Palestine over time, broken down by religion:
During the War of Independence, Israel grew rapidly as almost 110,000 Jews made their way to the new country, and nearly 620,000 had followed them by 1952. Different Jewish groups came from different countries, as the chart below indicates:

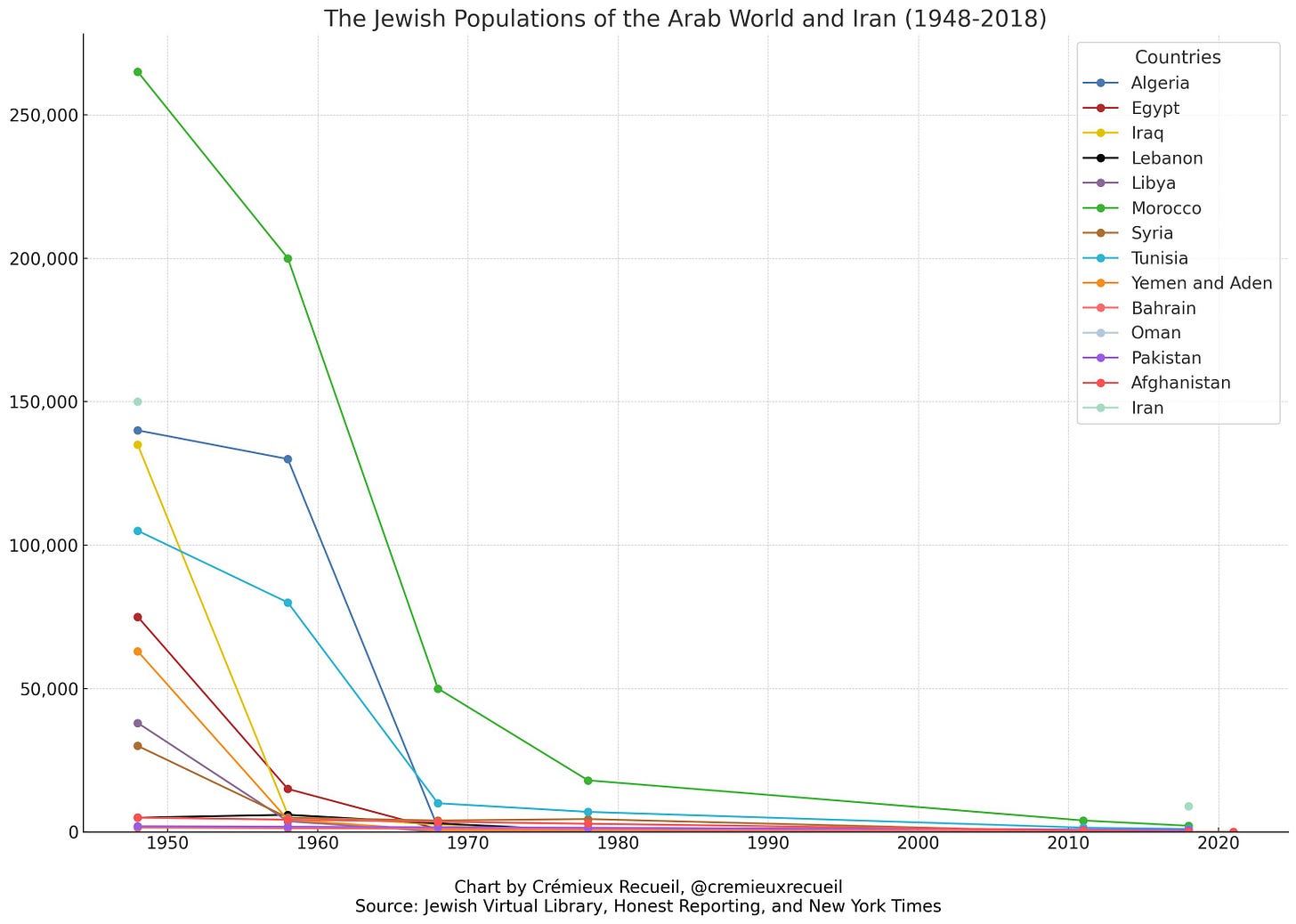
One might infer from this chart that Israel is mostly Ashkenazi. After all, two of the largest migration flows were primarily Ashkenazi. But this is misleading because Mizrahi immigration greatly increased after 1948. More than 850,000 Middle Eastern Jews were forced out of the Arab countries and Iran, which is why all these Jewish groups now reside in Israel.
Knowing about this early immigration and the fact that Mizrahim have higher fertility than Ashkenazim, while looking at Israel’s full immigration history by source country, we can see that Israel must be majorly Mizrahi. Even the much-discussed largely non-ethnically-Jewish Soviet immigration that happened after the Soviet Union fell is recent and their contribution to Israel’s population must be comparatively small because they’ve been in Israel for less time, meaning that they’ve had less time to have kids.
So what are Israel’s demographics? Drucker (2006) estimated that 61% of Israel’s Jewish population had full or partial Mizrahi ancestry. Lewin-Epstein and Cohen’s (2019) had 44.9% who were Mizrahim, 31.8% who were Ashkenazim in, 12.4% who were Soviet, 7.9% who were mixed and 3% who were Ethiopian in their sample. Lynn estimated that European Jews and non-Jewish Russians comprised 40% of Israel’s population, Oriental Jews comprised another 40%, Ethiopian Jews comprised 1.3% of the population, and Arabs comprised 20% of the population. These estimates do not completely concur and there are no official statistics. Due to ethnic mixing and personal misidentification (as when non-Ashkenazi Soviets identify as Ashkenazi, or mixed people identify as completely belonging to one category), misclassification risk in Israel-based studies is a major problem.
For estimating the IQs of Arabs in Israel, we have the studies by Leiblich & Kugelmass (1981), Zeidner (1987; four results), Werner (2003), and Martin et al. (2004; two results). The first study had 2,111 Jews and 639 Arabs and found an Arab IQ of 86 relative to a Jewish IQ expressed with a mean of 100 and a standard deviation of 15. The next study involved four tests given to university students, and thus it’s range restricted, but it nevertheless found Arab IQs of 87 to 92. The third study was based on the results of a knowledge test about osteoporosis given to people at an outpatient clinic, and it supported an Arab IQ of 87. Martin et al.’s results came from the mathematical and reading tests for the Third International Mathematics and Science Study, and they supported Arab IQs of 80.05 and 89.35. The simple average of these results is 87.7. And when including the means of the studies with repeated sampling, the average is 86.9. The meta-analytic mean is 87.4 or 85.5 without the university sample. Ofek-Shanny (2021) collected data that could be used for estimating Arab and Jewish IQs. Yet their results imply that Jews are just 9.4 points ahead of Arabs, and that U.S. Whites are just 9.7 points ahead of U.S. Blacks, which suggests the test in question isn’t very g-loaded, the samples were in some way selected, or there were errors in calculation.
For estimating the IQs of European as opposed to Oriental Jews there are quite a few studies: Smilansky (1957; three results), Ortar et al. (1966; two results), Leiblich et al. (1972), Gill (1974), Smilansky et al. (1976), Gross (1978), Burg & Belmont (1990; five results), Zeidner (1987; four results), Rim (1983), Ortar (1967), Smilansky & Yam (1969; two results), Levy & Chen (1976), Smilansky & Shefatiya (1977), Levi et al. (1978), Chen et al. (1978), Eshel (1980), Chen et al. (1983), Zuzovsky (1987), Levin (1988), Chen (1987), Minkowitch, Davis & Bashi (1982; six results). Several of these are missing sample sizes, so can’t be included in the meta-analysis. The simple average estimate of the Oriental Jewish IQ is 89.4 or 88.8 when including the means of the studies with repeated sampling. And the meta-analytic mean is 87.7. Yet some studies are problematic. For example, Burg & Belmont’s sample was matched for SES, which will have artificially reduced the gap. And Zeidner’s sample comprised of university students, which will have had introduced range restriction. Dropping these samples, the meta-analytic mean becomes 86.8.
Ethiopian Jews are the lowest-performing of the major groups in Israel. They’re overrepresented in prisons, among delinquents, among the unemployed, and among educational low-performers. This group has been given a variety of tests over the years. Kaniel & Fisherman (1991), Kozulin (1998), and Tuzuriel & Kaufman (1999) administered Raven’s matrices to samples of Ethiopian Jews, who achieved IQs of 68, 66, and 86 respectively. The Ministry of Education has reported other test results for this group – though unfortunately, without sample sizes. Since there are too few datapoints here for a meta-analysis, the simple average of the three Raven’s datapoints is 73.3, with the weighted average being 69.3. The simple average of all the Ministry of Education datapoints is 86.6; the simple average of all the Ministry of Education datapoints that are relative to Jews specifically is 86.2, and relative to Israelis as a whole, 88.4.
The Sephardim may be the smallest group depending on definitions, so their estimates are the least reliable and meta-analysis simply isn’t possible. Jordan (1921) assessed Sephardim and Russian Ashkenazim in the U.S., though the tests were likely biased given the immigration status of the samples. Ashkenazim had an average IQ of 101 and Sephardim an average IQ of 96.3. Based on slightly better samples, Gross (1969) found that Ashkenazim outperformed Sephardim by 0.58 g on the Stanford-Binet, 0.87 g on the Columbia Mental Maturity Test, 0.88 g on the Peabody Picture Vocabulary Test, while the Sephardim outperformed the Ashkenazim on the spatial Bender Visual Motor Gestalt test, by 0.39 g. These differences make more sense because Sephardim scored like Non-Jewish Whites and Ashkenazim scored like Ashkenazim. In a later study, Gross (1986) reported an estimate of 116 for Ashkenazim and 104 for Sephardim on the Stanford-Binet. The Serbian study by Lynn & Čvorović, mentioned earlier, is difficult to interpret but it seemed to find an Ashkenazi advantage. Overall, Sephardim seem to have an IQ like that of Non-Jewish Whites, at roughly 100 – perhaps without the spatial deficit of Ashkenazim.
There are also estimates for Israel based on tests with the WISC (Ortar, 1952), the Lorge-Thorndike (Miron, 1977), and Raven’s matrices (Moyles & Wolins, 1973; Globerson, 1983; Lancer & Rim, 1984; Tzuriel & Caspi, 1992; Lynn, 1994; Kazulin, 1998). These range from 89 to 97, with a simple average of 94.1 and a meta-analytic average of 91.5. However, they’re all over the place and we can’t be confident that they’re unbiased.
Now we need to estimate each of these groups IQs relative to a country like the U.S. We know that Arabs perform worse than Israeli Jews; that Ethiopian Jews perform worse than other Israeli Jews and Israelis as a whole; that European Jews outperform Oriental Jews; and that Ashkenazim likely outperform Sephardim. Aside from the possibility of selective immigration, we don’t have any reason to believe that non-Jewish Soviets perform better than Russians and or other Eastern Europeans in general. We also know that the aforementioned differences are unlikely to be environmental in origin: kibbutzim, where children were reared communally, showed the same European-Oriental gap. In fact, individuals on kibbutzim who had two European parents achieved an average more than a standard deviation higher than those who had two Oriental parents.
To obtain our final estimates, we need to establish constraints on what each group’s mean can be. The first constraint ought to be the Oriental-European difference, which appears to be on the order of one standard deviation. Yet this is likely to be an underestimate because some people belonging to one group may have been misclassified as belonging to the other or some other group entirely. If we assume the Oriental Jews are all Mizrahi and the European Jews are all Ashkenazi (ignoring Soviets), and we take Lewin-Epstein and Cohen’s (2018) estimates of the ethnic distribution of Israeli Jews, along with Drucker’s (2006) estimate of the proportions with full or partial Mizrahi ancestry, then some number of mixed people are identifying with the Mizrahi or Ashkenazi labels, causing misclassification bias, attenuating the group differences. If 7.9% correctly identify as mixed and the mixtures are just from these two groups, then an upper-bound on the attenuation without ability-related selective identification is 4.6 points given a Mizrahi mean (with misclassification) of 86.08.12 Let’s say the Oriental mean is 0.9–1.33 standard deviations below the European mean and the Soviets have an average IQ just above the Russian one, at 100. Now we can derive some constraints from the PISA examination (a constant source of confusion).
It’s common to hear that Israel’s PISA performance is underwhelming given the supposedly high intelligence of Ashkenazi Jews. But as I’ve noted repeatedly, Israel is not a purely or even largely Ashkenazi nation, so this is a non-sequitur. In fact, if we assign each of the relevant groups their canonical IQs, we can arrive at Israel’s PISA IQ of roughly 92.13 Using Lewin-Epstein & Cohen’s numbers: Ashkenazim are 31.8% of the Jewish part of the country with an IQ of 112; Mizrahim are 44.9% of the Jewish part of the country with an IQ of 82.5; mixed Israelis are 7.9% of the Jews with an IQ of 100; 12.4% of those who identify as Jews are Soviets with a mean of 100; Ethiopians are 3% of the Jewish population with a mean of 70; and Arabs are 20% of the total population with a mean of 82.5. This equates to an average IQ of 92.4. Israel’s comparatively low PISA is score is therefore perfectly consistent with high Ashkenazi intelligence. Moreover, this fits with two other constraints from the PISA: the 10th and 90th percentiles of Israeli scoring.
Many people are confused by what happens when you add up normal distributions that aren’t too far apart. The resulting distribution is generally not bi- or multi-modal. Under the preceding assumptions, the one for Israel looks like this:
The combined distribution is consistent with this commonly cited figure used to suggest that Israel’s 90th and 10th percentiles are somehow erroneous. In fact, Israel has the 90th percentile you’d expect for a nation with a mean of 100 and a standard deviation of 15 in this simulation. And Israel’s empirical 90th percentile is around the value for Italy, Iceland, Australia, Sweden, and Luxembourg. Moreover, Israel’s 10th percentile in this simulation is like Romania’s, with the latter’s national mean having been estimated at 86.9. If Israel had a mean of 100, the 10th percentile would be at 80.8. With a mean of 92, it would be 72.8, so the fact that it has a 10th percentile that is at Romania’s level empirically and in simulations suggests these simulation parameters aren’t too far off.
But we know Israel is one of the countries whose score on the PISA examinations is afflicted by substantial bias. Moreover, the assumptions made in the simulation above are not realistic given the relatively low fertility of secular Ashkenazim versus other groups like the Mizrahim. I say “secular Ashkenazim” because Israel also has many ultra-Orthodox Ashkenazim, who typically have extremely limited educations to the point where their test scores cannot be interpreted as representative of their abilities. Many of them do not learn to read or write adequately in the language of the test, and their mathematical education is almost never advanced. Ofek-Shanny recorded that in the 2015 PISA sample, ultra-Orthodox Ashkenazim constituted 610 of Israel’s 6,598 students. These demographic and cultural factors have the effect of artificially reducing Israel’s score.
Pokropek, Marks & Borgonovi (2022) have shown that the PISA examination largely reflects general intelligence. If we refit the 2015 data using the method applied to the Project Talent cohort – with reading, science and mathematics as lower-order factors, and g as a higher-order factor – then Israel’s true level of performance is equivalent to an IQ of 97.3, not 92 – and that’s without removing the ultra-Orthodox from the sample. (The empirical 10th percentile of performance is 73.4 and the 90th percentile is 120.1.)
If we re-run the simulation above with the constraints that Mizrahim need to be 1 SD below Ashkenazim, Ethiopians need to be 1 SD below the combined rest of the Jews14, and Arabs need to be 1 SD below all Jews, we could set the Ashkenazim to 110, the Mizrahim to 95 and the Ethiopians to 85.96, giving us an Arab IQ of 85.5. This delivers a simulated mean of 97.4, a 10th percentile of 75.1 and a 90th percentile of 119.7, which is probably close enough! The Israeli IQ riddle is effectively solved.
Despite this result, I still suspect Israel’s Ashkenazim are slightly less intelligent than their counterparts in the U.S. and U.K., because selective migration ought to have reduced their average. They do make up almost all the billionaires, selective prize winners, competitive game champions, actors, and intellectuals in Israel. But I have a niggling feeling that “it’s good to live like an American” reflects the feelings of many skilled Israelis, whose emigration disproportionately impacts the average IQ of Ashkenazim.
In any case, there is nothing about the performance of Israeli Jewry that stands out as being inconsistent with a high Ashkenazi mean IQ.
Why Are Jews So Successful?
It’s frequently said that Jewish success cannot be explained fully by IQ. In many domains, it obviously can. For example: chess, bridge performance, Wolf prizes, Nobels, Fields Medals, grades, and representation among significant public figures, are all domains in which Jewish excellence can be fully explained by IQ. And indeed, observed Jewish representation at one point in time provides psychometrically plausible estimates of Jewish ability.
But this may not be universally true. For example, can Jewish IQ explain the numbers of Jewish actors, middle managers, talk-show hosts, and so on? Perhaps not. After all, it’s not like people in those professions benefit enormously from an exceptionally high IQ. There’s certainly no way that high Jewish intelligence explains why Ben & Jerry’s, Häagen-Dazs and Baskin-Robbins were all started by Jews.
But there’s no need to jump from observations like these to an explanation for success like the one put forward by Kevin MacDonald. There’s no need to propose that any unexplained overrepresentation of Jews is due to ethnic nepotism on Jews’ parts. After all, Jews are disproportionately urban, they live in states that make it easier to attend elite schools, and they might have interests and personalities that are conducive to success-seeking. If the stereotype of Jews as being more concerned with money is correct (and most stereotypes are correct to some degree), then this could plausibly contribute to Jewish overrepresentation in certain domains. As Cofnas noted:
The fact that stereotypes tend to have a basis in reality (Jussim et al., 2015, 2016) and that Jews have been consistently stereotyped as having distinctive personalities—for example, as being “shrewd” (Brigham, 1971)—provides preliminary support for the hypothesis of personality differences … There is a whole constellation of psychological traits and mental abilities (which may be genetically or culturally transmitted) that contribute to success in any given domain. Jews (particularly Ashkenazim) were subject to evolutionary selection pressures—presumably the ability to succeed in white-collar professions (Cochran et al., 2005) and/or Talmudic study—that favored higher general intelligence (g). The same selection pressures would have favored non-g traits and abilities that contribute to success in business or scholarship … The achievements of East Asians testify to this phenomenon. In America, East Asians outstrip Whites in socioeconomic status far beyond what would be predicted based on their (at most) moderate IQ advantage (Flynn, 2008).
Some people have found that Jews have ‘better’ personalities in the form of higher scores on the ‘general factor of personality’15, but this has failed to replicate. Others have proposed that Jewish culture16 and Jewish values explain Jewish success. Given that Jewish success is a disproportionately or even exclusively Ashkenazi phenomenon, values-based explanations seem rather unconvincing. What’s more, in datasets like the General Social Survey, it is the less serious denominations (Reform) that achieve higher IQ and socioeconomic status and in Lasker & Kirkegaard (2020), the most religious Jews were the least intelligent.17
The recent decline of Jewish success is an important phenomenon, and it suggests Jews are like other groups: outbreeding tends to reduce their average success, as does higher fertility among the most religious and least professionally successful sub-groups. This, in turn, seems to suggests that Jewish success is “normal”. In fact, I would argue that basically every case of Jewish overrepresentation that people claim shows evidence of nepotism has an alternative explanation that’s more plausible. As the Tablet article mentioned at the beginning indicates, Jews may now be underrepresented in certain domains, relative to their abilities.
One amusing possibility is that Jews really do have poor spatial ability, and that’s a good thing! It has been shown that higher spatial ability is related to having different interests than the ones that are conducive to academic work, and that this, in turn, is associated with reduced educational success. If Jews are the “women of ethnicities” due to their relatively poor spatial ability (there’s a large sex difference in spatial ability favoring men), this may help them get ahead in modern society – if only because it leads them toward interests that are increasingly associated with success.18
What ultimately explains Jewish success will have to be discovered empirically. But I’m never surprised when a group with exceptional intelligence does well.
Cremieux Recueil writes about genetics, 'metrics, and demographics. You should follow him on Twitter for the best data-driven threads around.
Support Aporia with a $6 monthly subscription and follow us on Twitter.
As noted in Cofnas (2023), this includes the Japanese-controlled Kyoto Prize, which Jews win at the same rate as the Nobels and Fields Medals. Additionally, Cofnas noted that Jews win apolitical Nobels (sciences) at higher rates than political Nobels (peace, literature).
Given a standard deviation of 15, a single sample of this size would have 98% power to detect a difference of d = 0.1, or approximately seven times smaller than the observed Jewish advantage.
Given a standard deviation of 15, a single sample of this size would have 99% power to detect a difference of d = 0.43, which is about 75% as large as the observed effect.
Germany may fit the same pattern. Němeček showed that Jewish children obtained higher marks in German schools in his 1916 paper Zur Psychologie christlicher und jüdischer Schüler. (Because of range restriction, the estimates that can be derived from that paper are only directionally revealing.)
To obtain a crude IQ estimate from this result, we take the observed Jewish SAT score (1161) and that year’s White mean SAT score – which is upwardly-biased by the inclusion of Jews – and divide the delta by the norming standard deviation. This results in a Jewish advantage of approximately 0.5 standard deviations over Whites. Because of trends in scores that are sometimes attributable to changes in the workings of the test, it is not advisable to compare across years. So for example, in 1990 the Jewish mean on the SAT was 1030 and the White mean was 934, meaning Jews had a 0.48 standard deviation advantage. If this number had been compared to the 2002 number, however, one would spuriously conclude that Whites in general outperform Jews.
This study’s estimate is 109.7, but this is because they used the sample with genetic data. Including Jews and Gentile Whites without genetic data, the Jewish advantage drops to 0.47 SDs, or an IQ of 107.1. Since the Gentile White scores also dropped with this inclusion, the adjusted Jewish score such that Gentile Whites had an IQ of 100 increases to 108.4. Using non-public figures would not meaningfully change the result since this sample was so small relative to the complete meta-analytic sample.
There’s 99% power with a sample of this size to detect a difference as small as d = 0.044; hell, there’s 80% power to detect a difference of d = 0.029.
I suspect this has to do with both assortative mating and self-identification practices. American Jewry has become increasingly mixed, but the samples here generally deal with Ashkenazim who are likely to be fully/majorly Ashkenazim, whereas increasing numbers of self-identified Jews are only partially ethnically Jewish.
For the purposes of fitting a good model, I randomly split Non-Jewish Whites into two groups with as close to equal means and standard deviations for each of the subtests as possible, and I fit the g-VPR model to one of the Non-Jewish White subsets. The CFI for this model was 0.971, but it had several cross-loadings that were near-zero, so I pruned all nonsignificant cross-loadings, ending up with an initial CFI of 0.974. I then refit the same, pruned model on the other Non-Jewish White group. Since the model fit well (CFI = 0.973), I proceeded to fit it to each of the other groups individually and it fit well in every case.
After finding the initial g-VPR model, I began fitting a multi-group confirmatory factor analysis, or MGCFA. An MGCFA allows me to test for bias in the model’s measurement parameters—loadings, intercepts, residual variances, etc.—and it affords me a platform to test which of the structural parameters—latent means, variances, covariances, etc.—can be feasibly constrained without causing a drop-off in the quality of the model’s fit. A drop-off in model fit was indicated by sample size-adjusted BIC because the sample size for this model was extremely large, so any χ2 test result would be highly significant, even if it wasn’t practically significant or if bias wasn’t directionally consistent. For a simple primer on measurement invariance testing and estimating the effect size of bias in CFAs, see Fischer & Karl (2019). For work addressing the substantive implications of measurement invariance, see Lubke et al., (2003a), Lubke et al. (2003b), and Lubke & Dolan (2003).
The configural model fit was good (CFI = 0.969), and with that fit index, the metric model fit fine (0.964), but it showed non-negligible misfit and some loadings had to be freed. Between the Jewish White and Non-Jewish White groups, most loadings aside from those on spatial tests were fine; the subtests Math I and Word Functions in Sentences were strongly biased with respect to Blacks, while Disguised Words and Table Reading were strongly biased with respect to Asians. To minimize bias while avoiding freeing too many parameters, I adopted an approximate measurement invariance approach, where I checked the amount of bias attributable to a loading or an intercept being significantly different (≥50% SABIC weight preference for prior model) by freeing the parameter and estimating the impact of the difference on that subtest mean, keeping the parameter constrained if the bias was <0.03 d for loadings or <0.05 d in size for intercepts. When I did this, I freed the parameter and pushed it as far as it could go towards the value for the Non-Jewish White group (the largest group) without causing a significant reduction in model fit, defined by SABIC and p <= 0.001, arbitrarily. Since the intercepts for the Physical Science, Mechanics, and English Usage subtests were strongly biased (the first two, between Non-Jewish Whites, Jewish Whites, and Blacks, all three with respect to Asians), those had to be considerably adjusted (the scalar model had CFI = 0.966 relative to the adjusted metric model’s 0.967). The residual variances were unbiased in most cases, and only had to be freed due to large differences in the cases of Spelling, Visualization in 3 Dimensions, and Bible, resulting in a model with a CFI of 0.965.
The structural model where I assessed the equality of the latent variances was strongly rejected. This effect was so large that CFI dropped to 0.952. The best-fitting model (CFI = 0.965) saw the latent variances for the Mathematics, Verbal, Spatial/Reasoning, and Information factors constrained to equality and the other latent variances left freed. With respect to my primary focus, g, relative to a White standard deviation of 15, Asians and Blacks had an equal standard deviation of 15.538, while Jews had a standard deviation of 16.876. When I attempted to constrain all factor means, the CFI dropped to 0.912, and the best-fitting model (CFI = 0.963) ultimately constrained the Information, English/Mathematics, Spatial/Reasoning, Verbal, and Speed means to equality between most groups.
The most-likely reason this differs from modern Asian results showing larger advantages over Whites is due to differences in who is classified as Asian. Selective migration as a source of increasing IQs for Asians is also a possible explanation, but it seems unlikely given that national Asian norming samples show advantages over American and British ones.
With ‘pure’ individuals misclassifying, this bias could be even larger, but this estimate is probably fine, although the Mizrahi samples and the population totals come from different years, so there’ll be some error. There are too many possible values if identification of mixed individuals with source groups is nonrandom, so I won’t deal with that scenario.
It is worth noting that news sources like Weinglass (2017) – which are cited as evidence of Israeli underperformance – show scores for Hebrew speakers that are already on par with countries like Norway, Luxembourg, Portugal, and so on.
This assumption is almost-certainly generous to Ethiopians, whose abilities are overestimated by Ministry of Education data due to selective dropping out and selecting into unmonitored, low-performing schools.
That seems unlikely to exist, but it might reflect evaluative biases, generally more success-conducive personality, or even psychometric bias.
On the other hand, Dunkel (2014) found that a person’s parental Hebrew/Yiddish language proficiency was correlated with intelligence, unlike other forms of parental language proficiency. This proficiency variable is a means of defining Jews in Project Talent, so the result has no clear interpretation in the present context.













It's striking how physics is highly Jewish but astronomy is not, despite the two fields being closely related since Kepler and Galileo.
https://www.youtube.com/watch?v=uGkLjfPWqeI
I grew up in a majority Jewish area and I think the idea that Jews aren't nepotistic toward other Jews is laughable. The Jews I grew up with would feel the same. I don't know exactly how to rank Jewish Nepotism versus other ethnic nepotisms. Less than blacks or Indians, more than whites.
That doesn't mean there is a vast Jewish conspiracy to control the world, but the idea that everyone but Jews would have elements of ethnic nepotism seems absurd.