Twin Studies and the Heritability of IQ

Why the standard estimates are probably right.

Written by Coel Hellier.

Whether differences in intelligence are due to people's genes or their environments has long been contentious. One answer to this question comes from twin and adoption studies. By comparing outcomes for identical twins (who share all their genes) with those for fraternal twins and unrelated children, one can estimate the relative influences of genes in comparison with “shared environment” (all environmental factors shared by siblings growing up together) and “non-shared environment” (everything else, which can include things like randomness in embryonic development). Such studies give high estimates for the genetic contribution to intelligence, such that the heritability is between 50 and 70%.

A different method is to look directly at genes, through Genome Wide Association Studies (GWAS), which measure large numbers of genes in large numbers of people in order to estimate the genes’ combined effect on IQ. This method typically gives much lower estimates for the genetic contribution to intelligence, and the marked difference between estimates from twin studies and those from GWAS studies is referred to as the “missing heritability” problem.

Recently, the Harvard geneticist Sasha Gusev argued that twin studies are unreliable and the true heritability is close to the much-lower estimates from current GWAS studies. Claiming that "intelligence is not like height", he argues that, while height might be strongly influenced by genes, intelligence is not. “Adding up all of the genetic variants only predicts a small fraction of IQ score", he writes, adding that "the largest genetic analysis of IQ scores built a predictor that had an accuracy of 2—5% in Europeans”.

In response to Gusev's article, Noah Carl wrote a defence of twin studies. Here I add to that by arguing that current GWAS studies must be overlooking much of the genetic influence on intelligence. In short, intelligence must be affected by vast numbers of genes, which means that most of them must have very small effects, and current GWAS studies do not have the statistical power to detect these tiny effects. This is not a new suggestion (see, e.g., Jian Yang and colleagues’ 2017 paper), but it could well resolve the issue.

Being taught at school about Mendel and smooth versus wrinkly peas might leave the impression that traits can be determined by only one or a few genes. And while this might be true in some few cases, most traits are affected by very many genes. In particular, complex traits related to human personality and behaviour must involve huge numbers of genes (whereas a simpler trait like height could, in principle, involve fewer genes.)

Intelligence is among the most complex traits, which means that any genetic recipe for intelligence must contain vast amounts of information. If I asked you how many lines of code you'd need to program an intelligent robot you'd say, "Eek, millions at least!" Genes provide, of course, a developmental recipe rather than a direct program, but the underlying point—that this recipe must contain vast amounts of information and hence be encoded in tens of thousands of genes—still stands. It then follows that most of these genes must individually be having a very small effect. If N genes each contributed equally to intelligence then each would have a 1/N effect on the phenotype.

A basic rule of statistics is that to find smaller effects you need larger samples. Typically, the uncertainty scales as the square root of the sample size. So if an opinion poll samples 1,000 people then you get a 3% error range [sqrt(1000)/1000]. To do ten times better (a 0.3% error range) you'd need a sample size 100 times bigger. (You'd also run into systematic error, such as whether your sample is representative of the population.) And, of course, to find a tiny effect you need an error range smaller than that effect—preferably quite a bit smaller.

In writing about GWAS studies, I should own up that I am not a geneticist, but in my “day job” in astrophysics we have exactly the same problem. Which is why we build telescopes with large mirrors to collect many photons. We are studying tiny signals from faint galaxies at large distances in the universe, and every time we apply for time on a large telescope we calculate how much time we need in order to collect enough photons to have enough statistical power to find the small signal that we are looking for.

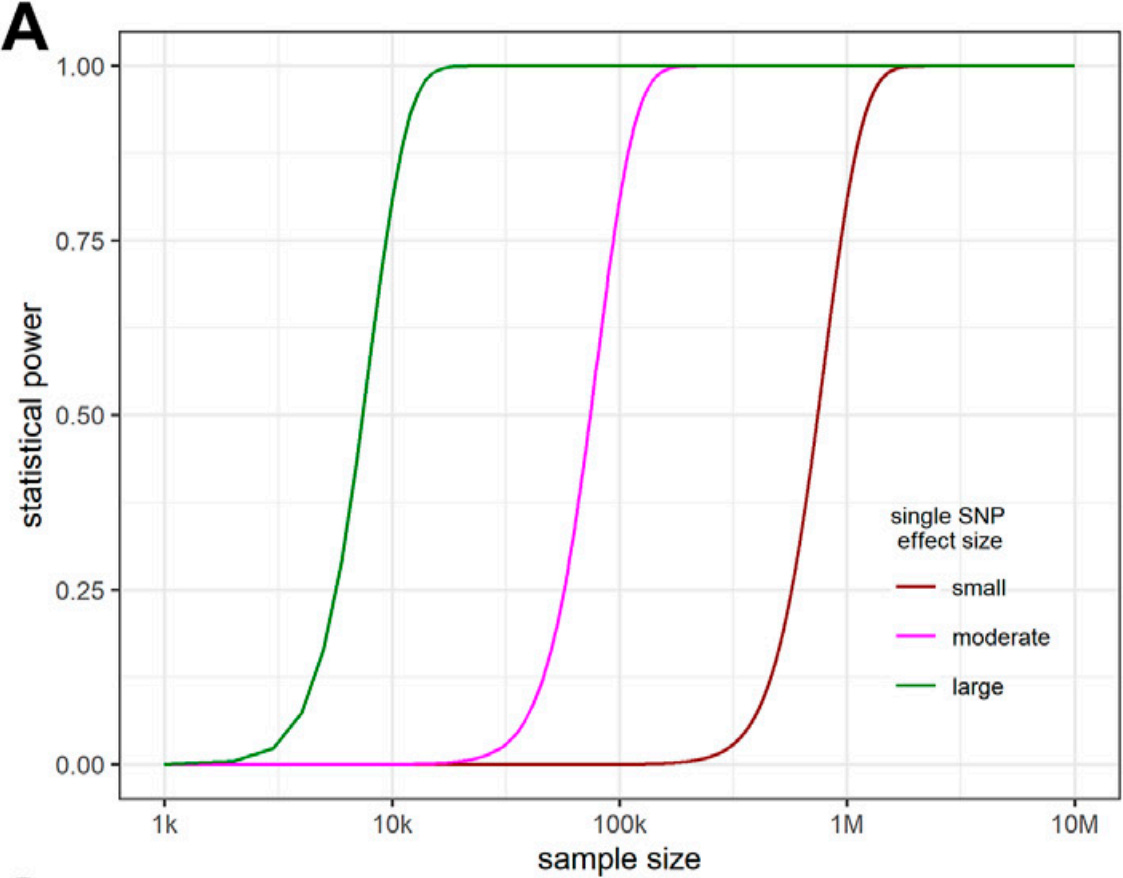
GWAS studies examine one type of genetic variability, Single Nucleotide Polymorphisms (or SNPs), and they typically record SNPs at 20,000 locations out of 3 billion nucleotides, analysing them in a sample of 10,000 to 100,000 genomes. For a discussion of the statistical power of GWAS studies I refer to the 2022 paper by Tian Wu and colleagues. As the authors confirm, "The statistical power for an individual SNP is determined by its effect size, the sample size, and the desired significance level. In a random sample of size n, the test statistic for the association between a quantitative phenotype and a SNP is β sqrt(n)", where β is the effect size. Making a range of assumptions, they develop a model leading to the following plot:

Power to detect an SNP of small, medium and large effect size. Source.

The plot shows the sample size (number of genomes) needed to find SNPs of small, moderate and large effect size, by which they mean 0.01%, 0.1%, and 1% of total SNP heritability. To have any chance of finding a gene accounting for 0.1% of the variance, you need a sample size of at least 30,000.

A similar paper that develops a statistical model based on a slightly different set of assumptions concludes that finding a SNP that explains 0.2% of the variance requires a sample size of at least 10,000, which is roughly consistent with the first paper. It's also worth remarking that real-life studies will almost certainly do worse than these estimates, since there are always sources of noise not accounted for in theoretical models.

Hence GWAS studies sampling tens of thousands of genomes could find the genes associated with intelligence if there were only a few hundred of them, but if they number a few thousand, then that requires hundreds of thousands of genomes at a minimum, and if intelligence involves over ten thousand genes then explaining all the variance is well beyond current GWAS studies.

The GWAS study in the quote from Gusev above sampled the genomes of 270,000 people. The authors do indeed report that the genetic differences they found account for only "up to 5.2% of the variance in intelligence", but they only found 205 "associated genomic loci" (blocks of SNPs associated with a trait). It seems wildly implausible that these 205 genetic differences are all that there is to a recipe for intelligence. (If you disagree, feel free to write down a program for an intelligent robot in only 205 lines of code!) It’s worth pointing out that AI models such as ChatGPT-4 are based on hundreds of billions of neural-network "weights" (though of course this is the end product, not the program itself).

Indeed a more recent and bigger study analysed 3 million genomes and found 3,952 SNPs associated with educational attainment, which together account for 12 to 16% of the variance. So (setting aside that intelligence and educational attainment are not quite the same thing), they have a larger sample, they find that many more SNPs are involved, and in total they account for a larger share of the variation.

Even then, this is likely to be merely the tip of the iceberg of genetic contribution to intelligence and educational attainment. There are 3 billion nucleotides in the human genome, and we have no good way of estimating what fraction of these might have some effect on intelligence. Further, GWAS techniques study only one type of genetic variation, the SNP, whereas there are lots of other ways in which genomes can vary. And, further, GWAS estimates assume a simple “additive” model, where the overall effect on the phenotype is simply the sum of the effect of each SNP individually. This could well be a good first-order approximation, but the developmental recipe for intelligence may involve myriads of subtle and complex interactions.

In short, since our understanding of the genetic developmental recipe for intelligence is close to non-existent, and since we are only guessing wildly at how many SNPs might be involved and how they interact, there is no way that we can conclude that current GWAS studies are picking up most of the relevant genes. Hence we cannot conclude that adding up the known effects gives anything like a true estimate of the heritability of any complex trait, including intelligence. All we can say is that it gives a lower limit.

Note that this argument is not attributing the missing heritability to rare genes of large effect, which, being rare, are simply not sampled in GWAS studies. (This idea used to be plausible, but is becoming less so as GWAS studies get bigger). Instead, it is attributing the missing heritability to large numbers of common genes that are sampled, but whose individual effects are too small to be detected with the statistical power of current GWAS studies.

In contrast, twin studies do not depend on knowing anything about how the genes produce intelligence. It is purely a suck-it-and-see method that takes whole genomes (from identical twins, fraternal twins and unrelated children) and measures the later-life outcomes.

Twin studies do have their own assumptions, including the "equal environments assumption". For example, do parents tend to treat identical twins differently from fraternal twins? This is one reason why the gold standard is studies of twins that were separated at birth and reared apart from one another. Twins being separated at birth is a rare occurrence today, but before the ready availability of abortion and the pill, there was a steady stream of young, unmarried mothers giving up babies to be adopted at birth, and it was common to separate twins. More recently, China’s one-child policy has led to twins being separated and adopted at birth and relevant studies give high values of around 0.7 for the heritability of IQ.

As a result of checks like this, heritability estimates from twin and adoption studies have been extensively examined and seem robust. We have no good reason to think that twin studies are severely overestimating the heritability of IQ. In contrast, there is good reason to suspect that the GWAS estimates are only a lower limit—and are currently much too low.

A slightly different version of this article was published here.

Coel Hellier is a professor of astrophysics at Keele University. You can find him on Twitter and Substack.

---

Support Aporia with a paid subscription:

You can also follow us on Twitter.