Written by Cremieux Recueil.
In 1980, concerned parents formed an advocacy group – Parents in Action on Special Ed. (PASE) – and sued the Chicago school system to put an end to the IQ testing of minority children. In the case of PASE v. Hannon, the group argued “on behalf of all Black children who have been or will be placed in special classes for the educable mentally handicapped in the Chicago school system.” Their principal argument was that IQ tests were biased, resulting in an abnormally large number of Black students being identified for placement into remedial education.
That word “bias” is frequently brought up when IQ tests are discussed. Yet I’ll wager that very few of the people who bring the word up can provide a coherent definition of it.
Bias does not simply mean that a measure gives different scores to different groups. This is one of the most common misunderstandings about “bias”. What it really means is that members of different groups obtain different scores conditional on the same underlying level of ability. To illustrate this, I’ve created a handy applet that you can play around with. The applet is explained in Footnote 1.1
The first scenario I will generate with the applet is one with unbiased measurement and no group differences in a measure we’ll call “ability”. To obtain the same results I do, set your seed to 1, use the supplied default measurement parameters, and set the means for both groups to zero. To quickly obtain these settings, you can select Preset 1 in the applet’s dropdown menu, set your seed to 1, and click “Generate Plot”. The other scenarios are given by the other preset options and can be accessed in the same way. The output for the first scenario should look like this:
The second scenario will feature Group A scoring substantially higher than Group B. The mean for Group A will be 1 instead of 0, but there will still not be any bias. It should look like this:
These two scenarios show that mean differences do not, by themselves, imply bias. After all, members of Groups A and B will tend to obtain the same score at the same level of ability even though they differ in their average levels of ability.
In the third scenario, there will be bias. Groups A and B will have the same underlying level of ability (0), but Group A will have its intercept raised from 0 to 1. So despite being just as able as those in Group B, members of Group A will tend to have higher observed scores at every level of underlying ability:
In the fourth scenario, observed scores for members of Group B will continue to be underestimated, but the slope for Group B will be adjusted from 1 to 0.6. Accordingly, the scores for members of Group B will be underestimated even more severely at higher levels of true ability.
Now consider a fifth scenario in which the slopes are identical again (1) and Group A has a mean of 1 versus Group B’s 0, but Group B’s intercept is shifted up from 0 to 1. As a result, Group A’s members have higher true ability, but the bias in favor of Group B results in the two groups having identical means for observed ability.
Bias can clearly both increase and decrease the measured differences between groups relative to what they would be in the absence of bias. And as we’ll see later, bias doesn’t necessarily have any effect on the differences between groups. But back to PASE v. Hannon.
PASE alleged that the IQ tests given to students in Chicago were biased against Blacks. They brought forward several witnesses who testified as such, including George Albee, who testified that IQ tests measure exposure to White culture; Leon Kamin, who testified that IQ tests measure differences in information exposure; and Robert Williams, who provided the only attempt to demonstrate that there was any bias in IQ tests. In other words: several of the plaintiffs’ witnesses claimed IQ tests were biased, but only one attempted to show they were biased.
The lack of evidence brought forward by the plaintiffs left the judge incensed. He wrote:
It is obvious to me that I must examine the tests themselves in order to know what the witnesses are talking about. I do not see how an informed decision on the question of bias could be reached in any other way. For me to say that the tests are either biased or unbiased without analyzing the test items in detail would reveal nothing about the tests but only something about my opinion of the tests.
The judge identified the need to analyze specific items to see if they were biased, writing:
Plaintiffs were ambivalent in their attitude toward the need to analyze the specific test items. On the one hand, they recognized the relevance of such an inquiry by presenting Dr. Williams' testimony concerning bias in particular test items. However, he testified about only a few of them. None of the attorneys for plaintiffs nor the attorneys for the Department of Justice were prepared to discuss specific test items during the day-long oral arguments at the conclusion of the case, even though I had indicated long before the conclusion of the evidence that I felt analysis of specific test items was essential to a proper understanding and decision of the case. I am not satisfied that any of the dozen or so attorneys who participated in the trial of the case have even read the tests. In response to a direct inquiry during final argument, some of them admitted they had not and the rest said they had "at one time, but not recently." Plaintiffs' attorneys, as well as one attorney for defendants, stated that they felt it was unnecessary to look at the tests.
And so, the right honorable judge proceeded to scrutinize every single item on the Stanford-Binet (1960 test, revised with 1972 norms), the Wechsler Intelligence Scale for Children (WISC), and the revised WISC (WISC-R). This is – to put it mildly – an incredible breach of confidentiality. Though it is also what makes the case uniquely revealing about the nature of test bias. These tests included a lot of items, so let's look through items from the first one, the "Information" subtest from the WISC-R.
(The examiner, showing the child his thumb, asks) "What do you call this finger?"
"How many ears do you have?"
"How many legs does a dog have?"
"What must you do to make water boil?"
To get the right answers on these, the child must respond “thumb”, “two”, “four”, and some permutation of “heat it”, including variations like “turn the stove on”, “cook it”, “put it on the stove”, “light a fire under it”, etc. Those questions were for children aged 6–7. For children aged 8–10, there were questions like:
“How many pennies make a nickel?”
“What do we call a baby cow?”
The correct answers are “five” and “calf”. For ages 11–13, kids were asked:
“How many days make a week?”
“Name the month that comes next after March.”
“From what animal do we get bacon?”
“How many things make a dozen?”
The correct answers were “seven” (unless they say “five”, in which case they are asked “How many days make a week counting the weekend?”), “April”, “pig” (or “hog”, “piggy”, or any permutation thereof), and “twelve”. Questions 11–30 were intended for 14–16-year-olds, and it was only at question 12 that the plaintiffs began to question the items. Let’s review.
Question 12 asked children “Who discovered America?” and acceptable answers included “Columbus”, “Leif Erickson”, “Vikings” or “Norsemen”, “Amerigo Vespucci” and, if a child says “Indians”, the psychologist administering the test is supposed to respond “Yes, the Indians were already there, but who sailed across the ocean and discovered America?” Williams took this to be “absolutely insulting” to Amerindian children “since it implies that the land where their forebearers resided needed to be ‘discovered’ by someone else.” And he also claimed the item was confusing, because “it is a contradiction to say that something was ‘discovered’ when it was already occupied.” This line of criticism did not include any details about how the item was biased against Black children.
Question 13 asked children “What does the stomach do?” and children were supposed to reply with some details about the function of the stomach “in digesting or holding food.” Williams “testified that many Black children answer, ‘It growls’” because they come from poor households. But Williams failed to recognize that the test manual accounts for this kind of answer, with children who provide it often receiving “equal” credit (if the response is too unwieldy, the item is marked “for later discussion when the child is evaluated for placement”). If Black kids responded that the stomach growls, they would not be penalized because test makers have always been aware that there are correct responses they might not have accounted for.
Question 14 asked “In what direction does the sun set?” Children can say west or point and they’ll then be prompted to name the direction. This is the only question that someone besides Williams criticized. Dale Layman claimed this question was biased because it would be “unfair for a child who lives in a high-rise housing project and has never been on the west side of the building to see the sun set.” This opinion was not justified based on Layman’s experience as an expert.
Question 21 asked “In what continent is Chile?” and Williams took issue with it because “That’s hardly our environment [referring to Black people]”. The issue with this response is two-fold. First, it is the twenty-first question, so a person who was believed to be retarded would likely not have gotten this far because they would have already gotten too many questions incorrect. Williams always ignored this fact. Secondly, inasmuch as the location of Chile is not a question that’s relevant to Black people, it’s also not relevant to the White people in American classrooms. This relates to the next question that Williams took issue with. Question 23 reads: “What is the capital of Greece?” Again, Williams testified that “Athens is not a part of our environment.” Likewise, it is not part of White Americans’ environment. Similarly, question 28 read “What are hieroglyphics?” and Williams responded that they are “still not a part of this culture”.
Question 24 asked “How tall is the average American man?” Williams didn’t attack this question from the obvious angle that there are racial differences in heights (which the test accounts for within reason), but from his belief that it fails to “test a child’s ability to cope with his environment”. This is an odd criticism because it is hard to imagine someone coping with their environment without absorbing information about it.
Question 29 asked “Who is Charles Darwin?” and Williams responded that this was biased because Black kids ought to be asked about Black figures, not Englishmen. But again, the White kids were not Englishmen either. Williams also claimed that the item was biased because Darwin had negative opinions about Black people. He did not clarify why he thought that would make the question biased, but it also doesn’t matter because this was the 29th question, so a child suspected of being retarded would almost certainly not reach it anyway.
The judge continued going through each item in the tests, and Williams occasionally took issue with them, but the substance of his criticism was rarely serious. For example, in one case, he criticized “umbrella” as a vocabulary word because Black people were apparently more likely to use the word “parasol”. One of his few good criticisms was in response to the question “Why is it usually better to give money to a well-known charity than to a street beggar?” This question is scored zero if the child responds, “If you give it to a beggar, he is liable to keep it himself.” Because that’s “what you want the beggar to do”, he argued, “such a response is not inappropriate.”
Ultimately, the judge found there to be one biased item in the Stanford-Binet, and a total of eight biased items across the WISC and WISC-R. He concluded that “the possibility of the few biased items on these tests causing an [educable mentally handicapped] placement that would not otherwise occur is practically nonexistent.” He took greater issue with the plaintiffs’ theory of the case, writing:
They contend that the difference [in mean scores between Blacks and Whites] is entirely due to cultural bias. The implications of the argument are striking. Plaintiffs' hypothesis implies, for instance, that of the 328 items on the WISC-R, spread across twelve sub-tests of different kinds of subject matter and standardized on a sample that included representative numbers of blacks, there is not a single item which is not culturally biased against blacks. That such a thing could happen by chance, or because of simple inadvertence on the part of the psychologists who devised the test, is difficult to believe. No statistical evidence was presented on the question, but it seems highly unlikely that if mere inadvertence were involved, at least a few culturally fair items would not have found their way onto the test simply by chance. The strain on the laws of probability does not, of course, end with the WISC. The plaintiffs' hypothesis also includes the Stanford-Binet. This is a separate test, devised at a different time by different people according to a different format than the WISC tests. The Stanford-Binet contains 104 items spread over the seventeen sub-tests ranging from age 2 years through average adult. Each one of them according to plaintiffs' theory, is culturally biased against blacks.2
At this point, it’s fair to ask why the plaintiffs believed they could win in a case alleging IQ tests are biased when scrutiny of their items reveals them to be almost wholly unbiased. The reason is simple: their same arguments worked the previous year in the case of Larry P. v. Riles. The judge in that case was not like the judge in this one because the former did not think to examine the content of the tests. Because the judge in PASE v. Hannon had the good sense to know that a judgment of bias cannot be rendered from verbal arguments alone, he embarrassed Kamin, Berk, Stoner, Albee, and most of all Robert Williams. And all he had to do was give the tests a fair hearing.
For background, Robert Williams is a psychologist with two main claims to fame. The first is that he coined the term “Ebonics” (a portmanteau of “ebony” and “phonics”). This term was meant to denote the ways Black people in the U.S., Caribbean, and West Africa speak. Williams’ second claim to fame was the creation of a culturally Black test, the “Black Intelligence Test of Cultural Homogeneity” or BITCH (I’m not kidding). The National Institute of Mental Health provided Williams with a $153,000 grant to develop the test so that he could show it was possible to devise tests that were culturally fair for Blacks but not Whites (he alleged the opposite was true of typical IQ tests). Williams’ BITCH, however, was not a valid test. As the judge in PASE v. Hannon noted, “It would be possible to devise countless esoteric tests which would be failed by persons unfamiliar with particular subject matter…. The fact that it would be possible to prepare an unfair test does not prove that the Wechsler and Stanford-Binet tests are unfair.”
Williams’ goal was to prove there was racial bias in IQ tests, but despite this being one of his major career interests, he simply couldn’t do it. Through all the incoherent arguments, he could only show bias for nine items across the Stanford-Binet, WISC and WISC-R. But – and this is critical – even what the judge was willing to concede to Williams was too much. Four years after the case had been decided in favor of the defendants3, Koh, Abbatiello and Mcloughlin tested whether seven of the items identified as biased on the Information and Comprehension subtests of the WISC were actually biased in the ways Williams suggested. Using a sample of Chicago public school students who were in the sample considered by the judge, they found that none of the items disadvantaged Blacks. Three of the “Black” answers Williams supplied were more often given by White children!
What happened in PASE v. Hannon is not abnormal – quite the opposite, in fact. When experts allege that tests are biased, they are usually wrong. Even experts who have dedicated a substantial portion of their careers to the topic of test bias still have little luck finding any. Yet claims that tests are biased are still widespread, and they matter: tests are sometimes pulled over potential bias even when there isn’t any.
Sometimes Bias Doesn’t Matter
As noted above, bias means that members of different groups with the same levels of ability have different probabilities of providing the correct answer on a test.4 A lack of bias means that groups must have the same probability of acquiring knowledge that tests require. It also means that group differences must be driven by the same factors that driven individual differences. In other words, zero bias is only found when group differences are a subset of individual differences and all the causes of within-group differences are shared between groups and are, indeed, the drivers of between-group differences.5
Bias is clearly of great theoretical importance and its absence has big implications for group differences. But even when bias is present, it might not mean the test is systematically biased against one group. Many of the methods for detecting bias also allow practitioners to see the direction of bias, and there’s no guarantee that bias only goes one way; in fact, there can be similar numbers of questions with similar levels of bias against both groups, such that when the score for an entire test is added up, there’s no net bias.
Kirkegaard (2021) analyzed bias with respect to sex in a 45-item vocabulary test. He found thirteen biased items, but seven were biased in favor of men and six in favor of women. If you add them all up, the net bias was 0.05 d in favor of males (less than one IQ point).
Restrepo et al. (2006) analyzed bias in the Peabody Picture Vocabulary Test III (PPVT-III) and found three items that favored Whites and seven items that favored Blacks out of a pool of 72 in total. Webb, Cohen and Schwanenflugel (2007) also examined the PPVT-III. They found one item that appeared to be biased in favor of Blacks but that instead happened to favor low-ability children regardless of race.
Trundt et al. (2017) performed a multi-group confirmatory factor analysis (MGCFA) and found that the Differential Ability Scales, Second Edition (DAS-II) were largely unbiased with respect to race, but there was one subtest with a biased intercept that boosted Black scores by three points relative to Whites.
Odell, Gierl & Cutumisu (2021) examined measurement invariance in 47 PISA-taking countries’ 2015 performance on two objective tests (the mathematics and science scales) and one subjective measure (self-reported information and communication technology (ICT) familiarity). 68.60% of the intercepts and 34.80% of the slopes for the measurement model of the ICT self-report were biased. For the mathematics scale, 9.40% of the intercepts and 6% of the slopes were biased, whereas for the science scale just 0.83% and 1% of the intercepts and slopes were biased. Overall, then, it’s not advisable to compare PISA takers across countries when it comes to the subjective measure, but their mathematics and science performance generally can be compared.
In the context of tests’ predictive validity (i.e., the extent to which they predict outcomes like educational attainment or job performance), Roznowski and Reith (1999) showed that biased items do not necessarily cause biased prediction.
Unlike IQ tests, things like the personality scores used by Harvard’s admissions departments are often clearly biased.6 Interviews can also be biased, such as when they allow for caste-based discrimination in the hiring process.7 Writing tests like the one that used to be a mandatory part of the SAT – which produced smaller race gaps than the objective subtests – are also biased not just by race (in a way that reduces observed differences) but also seemingly by class.
One could go on and on with these studies. Meng Hu has done so. The conclusion reached by Valencia and Suzuki in their book Intelligence Testing and Minority Students still holds today: “Compared to the flurry of research activity during the 1970s and 1980s, very little research was undertaken during the 1990s. It appears that such a precipitous decline is related to the high percentage of earlier studies that had findings of nonbias.”
It may be boring to continue discussing how little bias there is in aggregate. Here I will review cases where experts proposed there was bias, or acted like bias went in a certain direction, and then bias was tested for, or where people were asked to explain examples of bias.
Experts in What?
The evidence that bias can be predicted in general is very poor.
Hope et al. (2018) examined bias in a British postgraduate exam for internal medicine doctors, finding that only eight of 2,773 questions were biased. Of the eight items, seven had modest effects and one had a large effect. For race, one item favored Whites in general while another favored high-ability Whites. For sex, one item favored high-ability women and another favored men at all but the highest levels; another two items favored high-ability women, one favored women consistently, and a final one simultaneously favored low-ability women and high-ability men. A panel of ten clinicians was then tasked with explaining why these items were biased but none could provide a cogent explanation for a single item. Reading the questions, it’s really no wonder bias was inexplicable.
O’Neill, Wang and Newton (2022) examined bias in 3,487 questions given to family medicine doctors in the U.S. between 2013 and 2020. They found that 374 questions were biased when Black, Hispanic, and Asian doctors were compared with White ones. But it’s unlikely that bias really made life harder for those doctors:
The items flagged as biased were reviewed by an expert panel including family medicine doctors, a linguist and a psychometrician. Out of the 10.7% of items that were found to be biased, the panel recommended that just four (0.1%) be removed from the examination item bank because of identifiable content bias. The panel simply couldn’t identify other biased items as being biased in any meaningful sense.
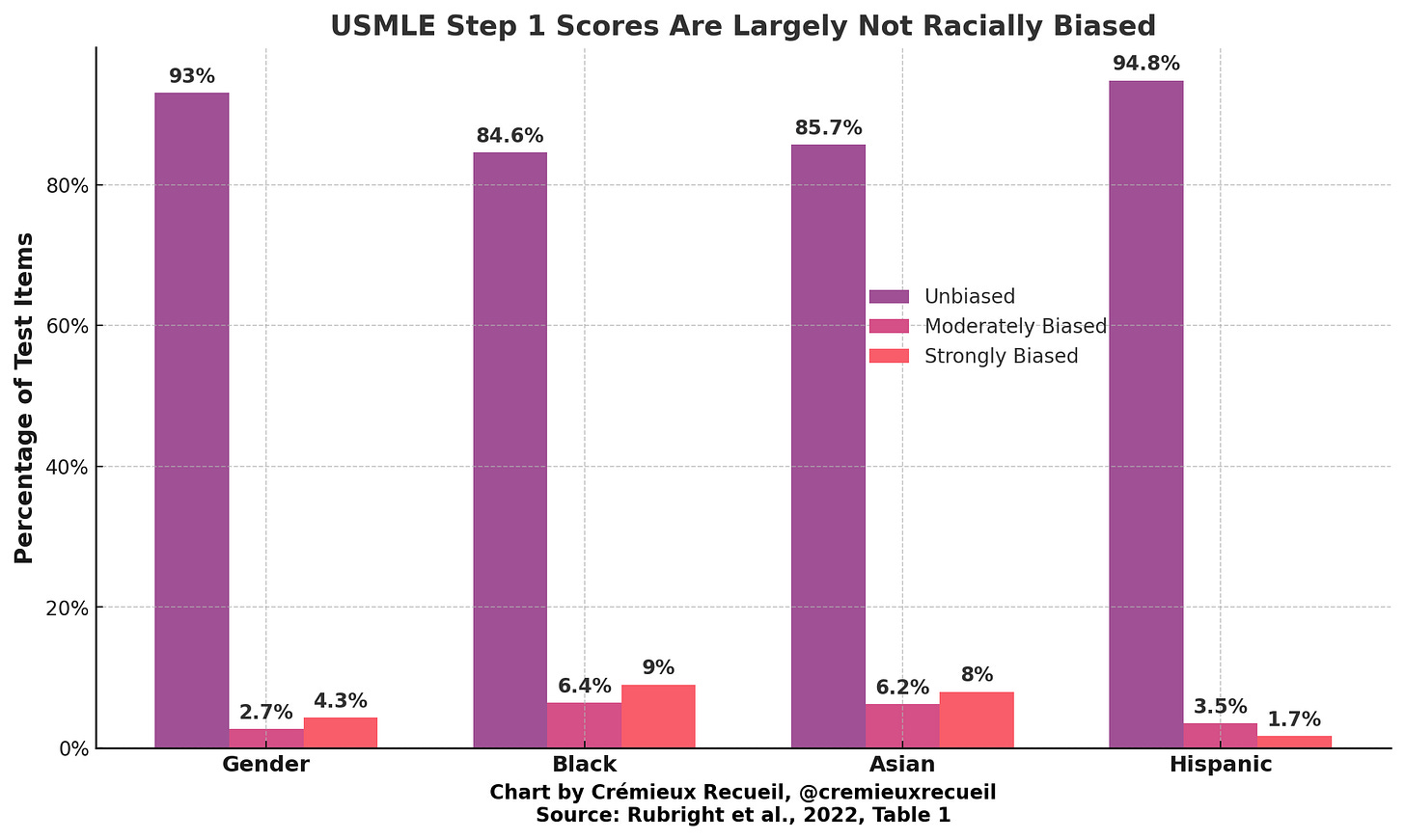
The U.S. Medical Licensing Examination (USMLE) Step 1 examination has come under fire in recent years. Not too long ago, it was turned from a continuous score into a pass/fail paradigm for reasons having to do with “diversity”. This examination, along with the Step 2 CK and Step 3 examinations, produce racial gaps that are similar in size to those found with other examinations, so there doesn’t seem to be anything unusual about them.8 Nonetheless, these gaps have led people to call into question the racial fairness of the USMLE Step 1 examination. One group even proclaimed that the examinations were biased seemingly because Blacks score lower than non-Blacks on them and their scores are normally distributed. The controversy around this examination has resulted in one of the best examples of the unpredictability of bias.
Rubright et al. (2022) examined whether items on the Step 1 examination were biased, resulting in 715 male-female comparisons, 78 Black-White comparisons, 386 Asian-White comparisons, and 116 Hispanic-White comparisons. The numbers of non-negligibly biased items were:
Subject matter experts were tasked with identifying which items were biased, and these were compared with the items’ actual bias (in the sense of differential item functioning). In this table cross-tabulating the results, the reference groups are Whites for race/ethnicity comparisons and males for sex comparisons. Experts did not hold up well.
Out of fifteen unbiased items, experts identified four as biased. Out of twenty-six items favoring the focal groups, they identified nineteen as unbiased, five as favoring the focal group, and two as favoring the reference group. Out of thirty items favoring the reference group, they identified twenty-six as unbiased and the other four as favoring the focal groups. Where they were correct about bias, it was obvious because the items were about women’s health issues and favored women – but that was an exceptional, predictable minority of the cases. Overall, the experts were correct about bias in just 22.5% of cases – worse than chance. Interestingly, even though 58% of the biased items favored reference groups (Whites, Males) and thus 42% favored focal groups (Blacks, Hispanics, Asians, Females), the experts managed to predict that 73% of the items they thought were biased favored focal groups.
There are many examples of psychometricians and psychologists who should know better drawing incorrect conclusions about bias. One quite revealing incident occurred when Cockcroft et al. (2015) examined whether there was bias in the comparison of South African and British students who took the Wechsler Adult Intelligence Scales, Third Edition (WAIS-III). They found that there was bias, and argued that tests should be identified “that do not favor individuals from Eurocentric and favorable SES circumstances.” This was a careless conclusion, however.
Lasker (2021) was able to reanalyze their data to check whether the bias was, in fact, “Eurocentric”. In 80% of cases, the subtests of the WAIS-III that were found to be biased were biased in favor of the South Africans. The bias was large, and it greatly reduced the apparent differences between the South African and British students. It also wasn’t confined to the most “cultural” subtests on the WAIS-III. The test’s Matrix Reasoning, Information, Comprehension, and Arithmetic subtests favored the South Africans, while the Similarities subtest favored the British group. The bias in favor of the British group was 1.13 d, whereas the bias in favor of the South African group was 0.79 d for Matrix Reasoning, 1.62 d for Information, 0.81 d for Comprehension, and 0.59 d for Arithmetic. There was bias, but rather than being “Eurocentric”, it might more aptly be dubbed “Afrocentric”.
Another example of psychometricians making incorrect claims about bias comes from Modgil and Modgil’s Arthur Jensen: Consensus and Controversy. Lorrie Shepard had claimed that that seven of thirty-two mathematics items given to high school seniors favored Whites over Blacks. She claimed that the removal of these seven items reduced the Black-White gap from 0.91 to 0.81 standard deviations. However, as Robert Gordon noted in the same volume, she forgot to remove the three items that were biased against Whites: “Her paper seems to suggest that such one-sided exclusions might be acceptable procedure… [but] this is simply not cricket. The suggestion itself and the use of such one-sided evidence against Jensen betoken desperation, all for a .1 sigma reduction.”9
A Final Word
Proposals that such-and-such a test is biased are almost always without merit. Test makers are simply too wise to the issue of bias, and they put in a great deal of effort to ensure their tests are fair. The same isn’t generally true for the makers of other questionnaires and selection instruments including personality tests, biodata keys, letters of recommendation, interviews, and so on.
If we want unbiased selection into academia and the labor market, all we really have are cognitive tests. The alternatives are all much worse, even if they sometimes manage to produce desired outcomes.10 As a final example, consider which is more biased when it comes to identifying gifted children: teachers and parents, or cognitive tests? (Hint: It’s not the tests.)
Cremieux Recueil writes about genetics, 'metrics, and demographics. You should follow him on Twitter for the best data-driven threads around.
Support Aporia with a $6 monthly subscription and follow us on Twitter.
The applet displays the relationship between group members’ “true” underlying levels of a trait and their observed levels of a trait. The default relationship between the true and observed scores is identical in both groups, but their mean “true” level is not. By default, the groups are differentiated by 1.1 standard deviations.
The slope denotes the linear relationship between true and observed scores. When it is equal for the two groups, it means they interpret the test questions in the same way, and when it is unequal, they interpret the questions differently across the range of the trait. Equality of this parameter is “metric invariance”.
The intercept denotes the level of the regression line between the true and observed scores. When it is equal for the two groups and metric invariance is observed, it means an observed score corresponds to the same ability level in each group, and when it is unequal, a given observed score corresponds to a different ability level in each group. Equality of this parameter is known as “scalar invariance”.
The standard deviation of the true score denotes the variance in the underlying trait for a given group, or the range of ability. The standard deviation of the observed score beyond the true score denotes the residual variance in performance for a given group. For this simulation, I have only allowed that to be an error term but setting it above or below the true score standard deviation makes it systematic with respect to the group that it has been altered in. This could represent many scenarios, like differential measurement error. In the real world it implies different causes are at work in different groups.
The applet contains the option to show points for the members of the different groups, to show their respective regression lines, and to show confidence ellipses containing 95% of the observations for both groups. The sample size is also configurable on a per-group basis and reproducible results may be obtained by supplying a seed for the random number generator.
Advanced users may wish to enter parameters that are outside of the range provided through the sliders. To obtain access to these settings, click the “Switch to Numeric Input” option at the top of the applet. Whenever a sample parameter is changed, the plot is not updated until “Generate Plot” is clicked.
To see an example of Kelley’s Paradox when measurement is unbiased but means differ and prediction intercepts thus differ, click the “Swap True/Observed Scores” button. For an explanation of this paradox, see here.
The plaintiffs also attempted to argue that the standardization process of exams was unfair, because exam makers “discarded items on which females did not do as well as males but did not discard items on which blacks did less well than whites.” They enforced this point by citing a study of sex differences where “about half the differences [between the sexes] went in one direction and about half in the other. The great bulk of items showed no differences.” The judge replied that “In the case of the racial differences, we are not talking about just thirty sub-items or even items. We are talking about all items on the tests. If all items on which the mean Black score is lower than the mean White score were to be eliminated, this would mean that the entire tests would be eliminated.”
Who were unprepared. In fact, they almost-certainly would have lost the case had the judge been complacent and less astute, like the judge in the previous year’s Larry P. v. Riles case.
Bias also occurs with respect to psychological instruments without objective answers, like personality tests. For example, imagine a relative height questionnaire is given in countries with different average heights. If individuals are asked “How tall are you relative to the average person?” they may compare themselves to their country’s average, resulting in a test that has a different interpretation across cultures. In cultures with different levels of sex-related segregation, people’s comparison groups may be more or less sex-specific, resulting in another comparison group-based difference in responding because male and female average heights differ.
This level of unbiasedness is strict factorial invariance, and it is the highest level of unbiasedness mentioned in this piece, though not the only level discussed in the relevant papers. Jensen dubbed this condition the “default hypothesis”. It is one reason why “culture” is a bad explanation for group differences. See Kush (2001, p. 84).
This level of unbiasedness also implies that when an intervention has differential effects by group (such as when it raises one group’s test scores but not another’s) then if that test was unbiased at baseline, the intervention biased it – potentially trivializing its effects because it is unlikely that induced psychometric bias has independent predictive power.
This makes Yale’s admissions seem biased as well.
Amusingly, Gordon also noticed that Shepard attempted to explain away the bias on this mathematics examination by suggesting that verbal reasoning was involved in the mathematics questions. Six of the seven questions biased against Blacks had verbal elements and one was numeric, while the three items biased against Whites were all numeric. Given a hypothesis that verbal items are biased against Blacks, one might expect to find that a verbal test was, accordingly, severely biased against Blacks. But Shepard’s own work showed “even less bias in an accompanying vocabulary test” that she chose not to focus on. Shepard even went so far as suggesting that intelligence tests were more biased than achievement tests because of g’s relationship to requiring test takers to make logical inferences, but again, her vocabulary test (a typically better indicator of g than mathematics performance) was practically unbiased. The case of Shepard shows that bias is hard to explain and hard to predict.
This often means something that has predictive power and also comes with small group differences simply because of bias.










You are being too kind.
I think it is more like:
“I don’t like the results, so the test must be biased.”
I recall the US government discontinuing its civil-service test (called PACE) in early 1980s because it was supposedly discriminatory (presumably against minorities). The inside joke amongst government new hires (who had to take this easy test) was that it discriminated against dumb people.